文獻標識碼: A
ΣΔ調制器采用過采樣和噪聲整形技術,已經廣泛運用在模數轉換器(ADC)中,它避免了元器件失配對ADC精度的限制,能夠實現高精度的ADC。ΣΔADC以速度換取精度,由于過采樣的特性,使得ΣΔADC只能用在低速、高精度數字信號處理如音頻處理等應用中,速度成為其更廣泛應用的瓶頸。
多通道時間交織技術采用多個并行工作在低速的系統來實現高速系統,已經在Nyquist ADC(如pipelined ADC, Flash ADC)中廣泛應用[1]。對于M通道的Nyquist ADC,M個通道工作在M個不同相位的時鐘下,如果每個通道的工作頻率為Fs,則整個ADC轉換速度為MFs,速度提高了M倍,實現了高速ADC。多通道時間交織技術是一種基于抽樣率變換理論的技術,通過下采樣和上采樣來實現的。ΣΔ調制器采用過采樣和噪聲整形技術,在抽樣率變換過程中,會出現信號頻譜的混疊和鏡像,所以,多通道時間交織的思想并不能直接應用到ΣΔ調制器中[2]。
本文從抽樣率變換和濾波器組基本理論出發,通過多抽樣率系統的恒等變換[3,4],推導了兩通道濾波器組無混疊的條件。對傳統ΣΔ調制器結構進行等效變換,得到兩通道時間交織 ΣΔ調制器的系統結構,理論上運算速度提高到單通道的2倍[5]。采用SIMULINK對二階兩通道時間交織ΣΔ調制器進行了建模仿真。
1 兩通道濾波器組

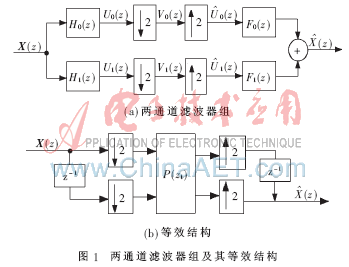

則其等效的兩通道時間交織結構如圖2(b)所示,此時該系統還是一個不可物理實現的非因果系統(系統環路包含非因果項z)。把非因果項z與每個通道的z-1項合并,得到如圖2(c)所示的等效結構。如果圖2(a)的系統工作頻率為Fs,圖2(c)等效結構量化器的工作頻率也為Fs。圖2(c)所示結構可以進一步等效于圖2(d)的結構,此時,除了采樣電路和輸出電路工作頻率為Fs,其他電路全工作的頻率是Fs/2。
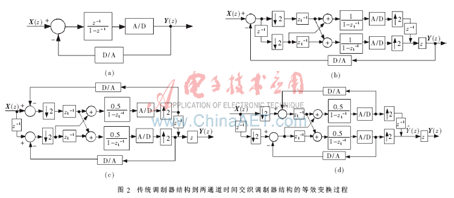
3 兩通道時間交織調制器結構及其仿真

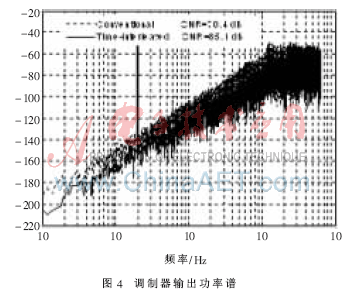
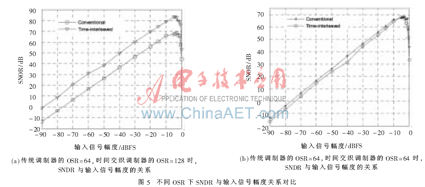
假設圖3(a)的傳統調制器工作頻率為Fs=64 MHz,圖3(b)兩通道時間交織調制器每個通道工作頻率也為Fs=64 MHz。采用SIMULINK分別對兩種調制器結構進行建模仿真,輸入信號為頻率Fin=1.9921875e+005,幅值為-4 dB滿刻度幅度的正弦信號,內嵌ADC與DAC為1 bit。兩種調制器輸出信號的功率譜如圖4所示,從圖4可以看出,兩通道時間交織調制器結構具有更好的噪聲整形效果。如果傳統調制器結構和兩通道時間交織調制器結構的每個通道的工作頻率相同,并且信號帶寬一樣,則兩通道時間交織調制器結構OSR為傳統調制器結構OSR的2倍,即相當于OSR提高了1倍。理論上,假設調制器的量化噪聲為白噪聲,根據ΣΔ線性模型,可以得到,調制器的OSR每提高1倍,其SNDR增加(6L+3) dB,其中L為調制器的階數[7]。圖5(a)為傳統調制器的OSR=64,兩通道時間交織調制器的OSR=128,即兩種調制器的信號帶寬一樣時,兩種調制器的SNDR與輸入信號幅值的關系。圖5(a)表明,兩通道時間交織調制器的SNDR比傳統調制器提高了大約15 dB,這與理論值相符。圖5(b)為傳統調制器的OSR=64,兩通道時間交織調制器的OSR=64,即兩通道時間交織調制器的信號帶寬為傳統調制器的兩倍時,兩種調制器的SNDR與輸入信號幅值的關系。從圖5(b)可以看出,當兩通道時間交織調制器的信號帶寬為傳統調制器的2倍時,其SNDR幾乎不變。這表明兩通道時間交織調制器的速度能提高1倍,而其精度不變。

本文在兩通道濾波器組無混疊的條件下設計了一種二階兩通道時間交織ΣΔ調制器,并采用SIMULINK對其進行了仿真。仿真結果表明:在不提高每個通道工作頻率的條件下,調制器的信號帶寬增加兩倍,調制器精度幾乎不變,相當于調制器的速度提一倍;如果保持信號帶寬相等,其SNDR能提高大約15 dB。在本文的基礎上,可以進一步對多通道時間交織ΣΔ調制器結構進行研究與設計。
參考文獻
[1] GUPTA S K,INERFIELD M A,WANG Jing Bo.A 1-GS/s 11-bit ADC with 55-dB SNDR,250-mW power realized by a high bandwidth scalable time-interleaved architecture[J].IEEE J.Solid-State Circuits,2006,41(12):2650-2657.
[2] Khoini-Poorfard R,JOHNS D A.Time-interleaved oversampling convertors[J].Electronics Letters,1993,29(19):1673-1674.
[3] 陶然,張惠云,王越.多抽樣率數字信號處理理論及其應用[M].北京:清華大學出版社,2007.
[4] VAIDYANATHAN P P.Multirate digital filters filter banks polyphase networks and applications:A Tutorial[J].IEEE Trans.Signal Processing,1990,78(1):56-93.
[5] BURRUS C.Block realization of digital filters[J].IEEE Transactions on Audio and Electroacoustics,
[6] SCHREIER R,TEMES G C.Understanding delta-sigma data converters[M].New York:IEEE Press,2005.
[7] 易婷.高性能Σ△模數轉換器設計[D],復旦大學博士學位論文,2002,3:17-19.

