文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.172072
中文引用格式: 趙黎,焦曉露,張峰. 基于前導序列的PLC系統定時同步技術研究[J].電子技術應用,2018,44(2):84-87.
英文引用格式: Zhao Li,Jiao Xiaolu,Zhang Feng. Research on the timing synchronization technology for PLC based on preamble sequence[J]. Application of Electronic Technique,2018,44(2):84-87.
0 引言
隨著智能電網和電力系統的飛速發展,電力線載波通信(Power Line Communication,PLC)技術備受關注[1-2],然而電力線信道環境惡劣,傳統單載波通信技術無法很好地抵御信道干擾,導致系統可靠性低,從而影響了電力線載波通信的應用和發展[3]。G3-PLC標準是一種電力線載波通信規范,已經被IEEE、ITU和IEC/CENELEC等主要機構所采納,可以有效地對輸電網絡、照明及智能電網應用進行管理、控制與監測[4],因此G3-PLC標準已成為面向智能電網通信技術的全球開放性協議[5-6]。
然而,OFDM系統的高頻譜利用率和傳輸可靠性都是以其子載波之間的正交性為基礎的,因此準確的符號定時同步技術是OFDM系統實現的關鍵。OFDM系統中的同步技術主要分兩類:(1)利用循環前綴的方法;(2)利用訓練序列的方法。當信道為嚴重的多徑衰落信道時,第一類方法會使部分循環前綴區間受到ISI破壞,使定時估計性能惡化,因此不適用于電力線載波通信系統中。第二類方法主要用于如無線局域網(WLAN)的突發式傳輸系統,估計精度較高,在多徑衰落信道下魯棒性能較好,最具代表性的算法為Stanford大學的Schmidl和COX D C于1997年提出的Schmidl&Cox算法[7],但由于自相關平臺效應,使S&C算法定時同步存在偏差。另一種經典的算法是Minn算法[8],雖然克服了S&C算法中符號定時測度的平臺效應,但是其訓練序列結構與G3-PLC標準的前導符號結構不相同,因此需要額外添加訓練序列,使系統有效速率降低。
因此,本文針對G3-PLC特有的前導符號結構,結合S&C算法的思想,提出了一種采用雙重相關算法實現定時同步補償的方法,并通過仿真對算法性能進行了驗證。
1 G3-PLC信號幀結構
一個完整G3-PLC的幀結構具體包括前導序列(Preamble)、幀控制頭序列(Frame Control Header,FCH)以及數據位(DATA)。如圖1所示,前導符號由8個SYNCP符號和1.5個SYNCM符號組成,其中每個SYNCP符號和SYNCM符號都包含256個采樣點,同時,接收端為了方便進行相位檢測,SYNCM符號相對于SYNCP符號有180°相位差。

FCH幀控制頭在前導符號之后,其包含了保證發送數據幀正確解調的必要信息。每一組數據幀中包含13個FCH符號,FCH之后是DATA數據信息,FCH本質上和數據位信息是一樣的,因此其中也包含了循環前綴,但由于其重要性,導致其調制方式不可調,只可采用最安全的DBPSK調制映射方式,各個FCH數據段和DATA數據段在加窗之后需要進行相鄰符號首尾重疊處理,重疊長度為8位。經過疊加之后,就形成了最后的數據幀。
2 雙重相關檢測同步原理
SYNCP符號中有用的采樣點碼元由36個子載波的相位調制產生,其對應的36個相位信息如式(1)所示:
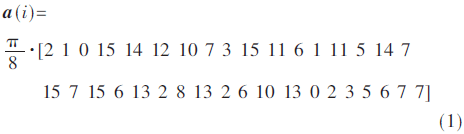
其中1≤i≤36表示有用載波序號。
將式(1)中的各個相位值在頻域建立對應的復數數據為:

式(2)中的復數數據經過IFFT變換就可以產生前導序列中的一個SYNCP符號,為了使產生的SYNCP符號實數化,需對式(2)中的復數數據進行相應的頻域編碼,首先將式(2)中的36個復數數據位插入到N/2(其中N=256)個子載波中的第23~58位,其余位數補零,如式(3)所示:
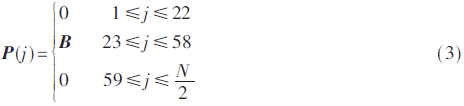
再根據FFT原理,將式(3)形成的N/2個子載波P(j)按照式(4)映射到N個子載波的前N/2位,再將P(j)的第2~N/2位的共軛倒敘映射到N個子載波的后N/2-1位,第N/2+1位置零:
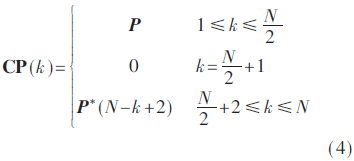
再對該N個信息數據進行N點IFFT變換,得到的SYNCP符號如下式,即為實數序列:
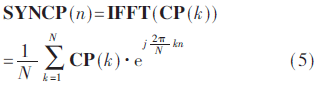
其中,0≤n≤N-1。
SYNCM碼元是由P碼元反相產生的,如式(6)所示:

在接收端,根據信道環境,在本地倒序選取一定長度的前導符號序列,假設接收端本地前導符號序列長度為發送端前導符號序列長度的1/2,即:
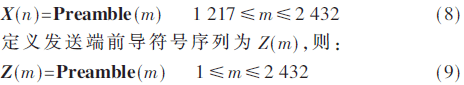
定義接收端經過信道干擾的產生失步的信息幀為Y(m),截取接收到的信息幀的前2 432位。
根據相關檢測原理,分別將Z(m)與X(n)和Y(m)與X(n)進行滑動互相關運算,即:


接收端通過對失步量進行補償即可精確地確定出每一幀信息中FCH位及DATA位的起始時刻。
3 系統性能驗證
為了驗證本文基于前導的G3-PLC同步算法性能,采用Monte Carlo方法對系統進行仿真驗證,結果如圖2所示,其中仿真參數設置為:子載波數目N=256,保護間隔的長度為CP=30,采樣頻域FS=0.4 MHz,SNR=-2 dB,符號偏差為399個載波符號周期,FCH符號數為NFCH=13,數據位采用DQPSK調制方式,FCH位采用DBPSK調制方式。圖2(a)為RZX(m)相關曲線,由圖可以得出J1=3 456;圖2(b)為RYX(m)相關曲線,其中J2=3 058,得D=J1-J2=398,與符號偏差值399差一個載波符號周期,在接收端通過補償即可判斷出正確的FCH位及DATA位的起始位置。

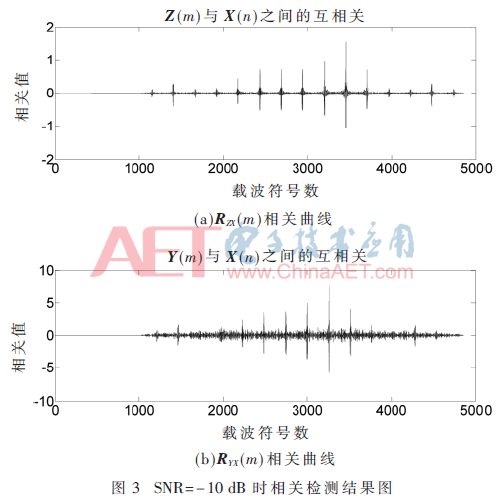
其他參數SNR=-10 dB保持不變,惡化信道環境設置,符號偏差為200個載波符號周期。圖3(a)為RZX(m)相關曲線,由圖可以得出J1=3 456;圖3(b)為RYX(m)相關曲線,其中J2=3 257,得D=J1-J2=199,與符號偏差值200同樣只差一個載波符號周期,在接收端通過補償即可判斷出正確的FCH位及DATA位的起始位置。
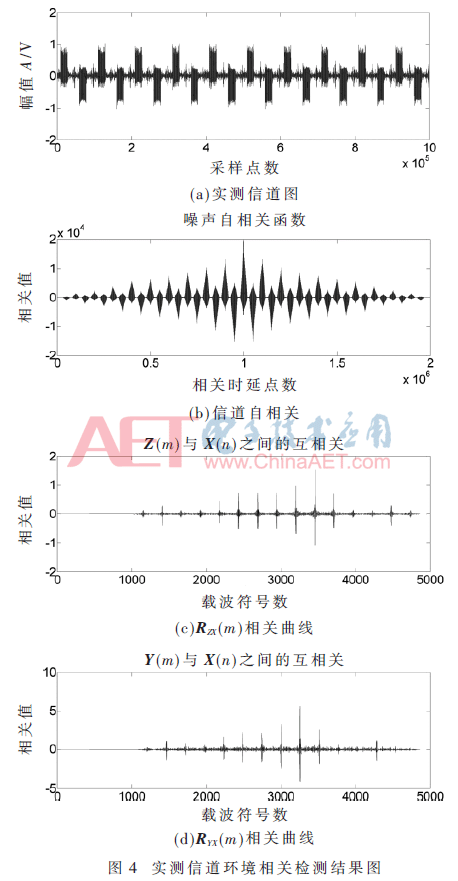
為了進一步驗證該算法對信道環境的適應性,其他參數保持不變,符號偏差為200載波符號周期,采用電力線載波實測信道參數環境,如圖4(a)所示為實測信道時域圖,由于電力線載波實際信道自相關曲線具有周期對稱性,如圖4(b)所示,因此其自相關程度近似為零,信號通過該信道后其相關性不會受到太大影響;圖4(c)為RZX(m)相關曲線,由圖可以得出J1=3 456;圖4(d)為RYX(m)相關曲線,其中J2=3 257,得D=J1-J2=199,與符號偏差值200同樣只差一個載波符號周期,在接收端通過補償即可判斷出正確的FCH位及DATA位的起始位置。
4 結論
由于低壓電力線建設初期并沒有考慮通信的要求,因此在傳輸信號過程中會受到噪聲、多徑干擾和頻率選擇性衰落等影響,造成定時同步不準確,在接收端產生漏檢和誤判。本文首先解析了G3-PLC電力線載波通信原理及G3-PLC信號幀結構,并根據G3-PLC電力線通信協議特有的幀格式,利用前導序列之間的相關性,提出采用兩重相關的檢測方法對系統的失步進行了有效的補償,并且最后通過Monte Carlo方法對系統進行了仿真驗證。結果表明,本文提出的系統同步補償算法對不同信道環境適應性好,可以準確地檢測到FCH位及DATA位的起始位置,使接收端能夠正確地解調信息,算法實現簡單,可靠性高。
參考文獻
[1] 辛耀中,石俊杰,周京陽,等.智能電網調度控制系統現狀與技術展望[J].電力系統自動化,2015,39(1):2-8.
[2] 王繼業,馬士聰,仝杰,等.中日韓電網關鍵技術發展及趨勢分析[J].電網技術,2016,40(2):491-499.
[3] RAZAZIAN K,UMARI M,KAMALIZAD A,et al.G3-PLC specification for powerline communication:overview,system simulation and field trial results[C].IEEE International Symposium on Power Line Communications & Its Applications.Brazil,2010:313-318.
[4] HOCH M.Comparison of PLC_G3 and PRIME[C].IEEE International Symposium on Power Line Communication and Its Application.Udine,2011:165-169.
[5] SOUISSI S,DHIA A B,TLILI F,et al.OFDM modem design and implementation for narrowband Powerline communication[C].International Conference on Design & Technology of Integrated Systems in Nanoscale Era,Hammamet,tunisia,2010:1-4.
[6] 李春陽,黑勇,喬樹山.OFDM電力線載波通信系統的定時同步和模式識別[J].電力系統自動化,2012,36(8):58-60.
[7] SCHMIDL T M,COX D C.Robust frequency and timing synchronization for OFDM[J].IEEE Transactions on Communications,1997,45(12):1613-1621.
[8] MINN H,ZENG M,BHARGAVA V K.On timing offset estimation for OFDM systems[J].IEEE Communications letters,2000,4(7):242-244.

