文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.171964
中文引用格式: 潘釗,張躍軍,丁代魯. 基于全同態MAC的消息認證算法設計[J].電子技術應用,2018,44(1):20-23.
英文引用格式: Pan Zhao,Zhang Yuejun,Ding Dailu. Message authentication algorithm based on fully homomorphism MAC method[J]. Application of Electronic Technique,2018,44(1):20-23.
0 引言
隨著電子技術和互聯網技術的迅速崛起,特別是云計算商業化平臺的出現,不安全信道中消息認證變得越來越重要。在消息認證過程中,通常采用構造消息認證碼(Message Authentication Code,MAC)的方式實現[1]。該方法可有效地檢測在傳輸過程中數據是否存在被篡改,目前已被廣泛應用在數字簽名、文件校驗、流密鑰產生等方面[2]。針對MAC算法的安全性、效率和能耗等問題,許多學者已經對此開展深入的研究。劉云璐等[3]提出一種消息認證協議優化算法,解決信息在樹狀傳感器網絡中的上層節點處擁堵和被丟棄的問題。王利村等[4]提出一種采用固定幀長的EPONMAC算法,使以太網交換機的速率得以提升。盧艷宏等[5]提出用于無線傳感器網絡數據傳輸的混合型消息認證算法,解決了能量損耗問題。但是,上述所提的方法均采用原始數據進行傳輸,存在消息被泄露的威脅。
近年出現的全同態加密技術,它允許對密文執行特定的操作后將其輸出進行解密,解密所得的結果與對明文進行相同操作的結果相等。全同態加密不但能夠提高數據處理效率、確保數據安全傳輸,而且可以有效避免將原始數據委托給第三方操作的安全問題。但是怎樣構造密碼體制使其具有全同態性質是學術界面臨的難題之一。2009年9月,GENTRY C等[6]在ACM計算理論年會上對“全同態加密”的可行性從數學上進行了論證,并給出具體實現方案,即在不解密的條件下對密文數據進行運算與對明文進行相同運算后加密的結果相同。DIJK M等[7]提出一種整數型全同態加密的優化方案,極大地簡化電路的硬件結構。鑒此,本文針對數據傳輸的安全問題,提出一種基于全同態MAC的消息認證算法,在SMIC 65 nm工藝下完成硬件電路設計。實驗結果表明,該結構不僅具有良好的黑盒性,還能夠檢驗傳輸數據是否完整。
1 全同態算法和MAC算法
1.1 全同態算法
在密碼系統中,設m為明文,c為密文,Enc為加密操作,Dec為解密操作,則有c=Enc(m),m=Dec(c)。在全同態算法中,設f為任意操作,則全同態過程可表示為Dec(f(Enc(m)))=f(m)或f(Enc(m))=Enc(f(m))。全同態算法主要包括密鑰的生成、加密和解密3個階段,具體如下所示:
(1)密鑰的生成。隨機產生一個密鑰p,且p為素數。
(2)全同態加密。對任意的明文m加密可得密文c=m+2r+pq。其中p為正的奇數,q為較大的正整數(比p要大,是否是奇數沒有要求),r為加密時由$random函數產生的較小整數(沒有正負要求),m為明文(m∈{0,1})。全同態加密完成對1位二進制數的加密,所得結果是N位整數。
(3)全同態解密。對任意的密文解密可得m=(c mod p)mod2。mod p表示以p為基數進行的模運算,可等效為以下運算:c mod p=c-「c/p」×p,其中「c/p」為c除以p的商取整。
1.2 MAC算法
MAC算法作為一種可攜帶密鑰的hash函數,通常用來檢驗所傳輸消息的完整性。常用的hash函數有MD5、SHA-2和SHA-3等,本文將采用MD5算法。MD5算法[8]可將任意長度的消息或文本進行相關運算,使其壓縮成128位固定長度的摘要,具體如下所示:
(1)補位。任意長度消息的低位用一個1和若干個0進行補位,在結果后面添加消息的最初長度(用64位二進制數表示),使消息長度剛好成為512的整數倍。
(2)初始化緩沖器。A1,A2,A3,A4是4個32位寄存器,也稱作鏈接變量的整數參數,并對其設置初始數據。
(3)非線性輪運算。聲明四個中間變量a1,a2,a3,a4,對其進行賦值:a1=A1,a2=A2,a3=A3,a4=A4。接著執行4輪主循環,每一輪完成16次運算,每輪用到一個非線性函數;每次操作需要對a1,a2,a3和a4中的3個變量完成一次非線性運算,并更新對應的變量數據。四輪非線性函數分別如下所示:

(4)數據輸出。當64步運算完成之后,將a1,a2,a3,a4分別與初始的值分別進行相加,然后對下一組512位數據進行運算,最后得到的結果為4個32位數據級聯構成的128位輸出,即32位16進制的MD5碼。
2 全同態MAC消息認證的VLSI實現
消息認證是指對要傳輸的消息或者和消息相關的信息執行一系列操作后再進行認證,目的是為了防止消息在傳輸和存儲過程中存在惡意篡改或錯誤修改,認證內容主要包含消息是否被篡改或延遲、消息是否來自真正的發送者等。圖1為消息認證系統的結構框圖。

2.1 全同態MAC的消息認證算法
全同態MAC的消息認證算法通過對消息進行全同態加密操作,再采用MD5算法對加密后的數據進行擾亂處理,不但避免在通信信道中傳輸原始數據的安全問題,而且能夠檢測消息有沒有被篡改,進而確保消息傳輸的可靠性。本文結合全同態算法和MD5算法,提出一種全同態MAC的消息認證算法,該算法的具體實現方案如下:
步驟1:將算法中輸入的二進制數據進行全同態加密處理得到密文。
步驟2:通過步驟1處理后,將數據經過MAC算法,使其生成MAC1值,將MAC1值及密文在信道中傳輸。
步驟3:接收方收到MAC1值和密文后,運用相同的MAC算法對密文進行運算,生成MAC2值,對比MAC1值和MAC2值,若一致,則用全同態解密算法對密文解密,恢復原始數據;若不一致,則接收方重新發送。
全同態MAC算法流程圖,如圖2所示。整個過程消息一直以密文進行傳輸,保證了原始消息安全性,只有當接收方確認消息來源和完整性后才進行密文的解密。全同態MAC算法的偽代碼,如圖3所示。其中,fhe表示全同態加密模塊,fhd表示全同態解密模塊,top表示全同態MAC算法模塊。


2.2 全同態MAC的消息認證算法硬件結構
全同態MAC的消息認證算法的具體結構如圖4所示。該算法首先執行全同態加密運算,將所得的結果經過數據控制模塊用1和0進行補位,并以信息長度為512位進行分組。每個分組又被分成16個32位子集,每個子集用Mj(j為0到15)表示,以新變量和子集作為輸入進行四輪主循環,每一輪循環需要完成16次迭代運算,其中每輪運算選擇一個不重復的非線性函數。第一輪選擇F(a2,a3,a4),則功能函數(a1,a2,a3,a4,Mj,g,ti)可表示為FF(a1,a2,a3,a4,Mj,g,ti),代表含義為a1=a2+(a1+(F(a2,a3,a4)+Mj+ti)<<<g),其中<<<g表示循環左移g位。每進行一次迭代,根據功能函數更新a1,a2,a3和a4中的一個,通過16次迭代后,得到更新后a1,a2,a3和a4的數值。然后,將更新后的數值應用于第二輪循環,以此類推,完成四輪循環;其次,將此時的a1,a2,a3和a4的數值分別與原來的A1,A2,A3,A4相加;最后,對下一分組數據進行相同操作,當所有分組都完成運算后,將新的A1,A2,A3,A4按順序級聯成128位數據輸出。

3 實驗結果與分析
采用SMIC 65 nm CMOS工藝,實現基于全同態MAC的消息認證算法硬件電路。實驗環境包括Intel Xeon(R) Dual-Core CPU 2.0 GHz、6 G RAM服務器,涉及的工具軟件包括:NCverilog仿真軟件和DC綜合工具。表1為p=11,q=121時,輸入數據經過全同態加密模塊的輸出數據。表2為p=11,q=121時,輸入數據經過全同態MAC算法的輸出數據。
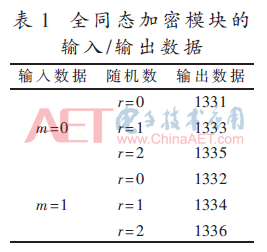
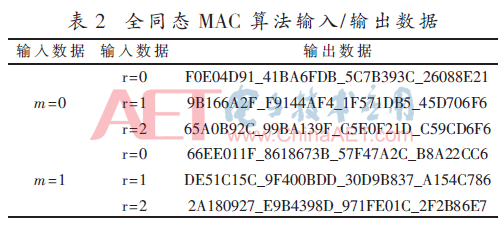
圖5為數據經過全同態MAC算法后輸出數據之間的相關性。其中,圖5(a)為同一組輸出數據的自相關函數,圖5(b)為6組測試數據之間的互相關函數。表明算法輸出數據具有良好的隨機特性。

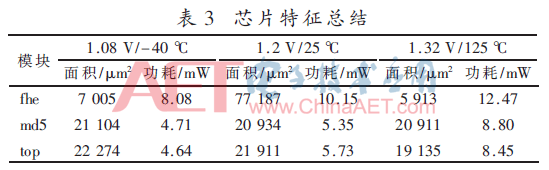
不同溫度/電壓下DC綜合的特征,如表3所示。其中,fhe為全同態加密模塊,fhd為全同態解密模塊,top為基于全同態MAC算法模塊。在1.2 V電壓下,DC綜合后電路面積為219 11 μm2,工作頻率最高可達到204 MHz,功耗為5.73 mW。
4 結論
本文通過對全同態算法和MD5算法的研究,提出了一個全同態MAC的消息認證算法設計方法。將全同態加密生成數據與原有的結果進行比較,驗證其黑盒性。實驗結果表明,該算法有效避免在通信信道中傳輸原始數據的安全問題,同時可以檢測消息是否被篡改,確保消息傳輸的可靠性。
參考文獻
[1] 徐津,巧燕,王大印.一種基于Hash函數和分組密碼的消息認證碼[J].計算機學報,2015,38(4):793-803.
[2] 張紹蘭.幾類密碼Hash函數的設計與安全性分析[D].北京:北京郵電大學,2011.
[3] 劉云璐,蒲菊華,方維維,等.一種無線傳感器網絡MAC協議優化算法[J].計算機學報,2012,35(3):529-839.
[4] 王利村,邱昆,王東,等.一種固定幀長的EPON MAC算法[J].電子科技大學學報,2004,33(6):730-733.
[5] 盧艷宏,掌明,馮源.無線傳感器網絡能量高效混合MAC算法[J].電訊技術,2012,5(8):1349-1353.
[6] GENTRY C.Fully homomorphic encryption using ideal lattice[C].Proceedings of the 41st Annual ACM Symposium on Theory of Computing,New York:ACM Press,2009:169-178.
[7] DIJK M,GENTRY C,HALEVI S,et al.Fully homomorphic encryption over the integery[C].Proceedings of EUROCRYPT’2010,Berlin:Springer,2010:24-43.
[8] 張裔智,趙毅,湯小斌.MD5算法研究[J].計算機科學,2008,35(7):295-297.

