文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.166484
中文引用格式: 唐焱,肖蓬勃,李發琴,等. 避障最優路徑系統研究[J].電子技術應用,2017,43(11):128-131,135.
英文引用格式: Tang Yan,Xiao Pengbo,Li Faqin,et al. Research of urban traffic obstacle avoidance and early warning system[J].Application of Electronic Technique,2017,43(11):128-131,135.
0 引言
隨著城市繁華區域車輛行駛密度的增加,行車過程車道上阻礙行車的各類移動、固定障礙物出現頻數不斷增多,嚴重影響行車速度,這是導致區域交通擁堵的主要因素之一。有關研究表明:駕駛者從觀測、判斷到駕駛動作的執行,以及車輛控制系統的反應,所需總時間在1.87 s以上,其中人員生理反應時間約占60%~70%[1]。因此在一定車速條件下,人工操作避障極易發生車輛與障礙物之間的碰撞,導致在車道障礙物較多的交通環境中難以實現自動駕駛。利用安裝于車輛前方的超聲波等探測系統進行路障信息采集,由車載電腦作數字化處理并及時反饋和視頻預警[2],將有效保證繁華市區行車安全和提高行車速度。
1 避障系統核心算法
1.1 人工勢場法
車輛行駛速度受行駛目的地、車道障礙物兩方面的因素影響。在繁華城區的行駛要求所有車輛能安全、迅速通過,從而對交通環境影響程度達到最小。人工勢場法原理表明,動態物體在設定的空間按預期目的地運動時,存在兩種物理勢場的影響,即預期目的地吸引力和運動過程沿途障礙物的排斥力。運用多目標優化處理的方法,合理解決上述吸引和排斥的矛盾,能獲得安全高效的運動方案[3]。
1.2 A*搜尋算法
A*搜尋算法是一種探測性的算法,其是一種在平面圖形中求出最低成本的算法。規劃合理的行車路徑,減少擁堵,降低運營成本是A*搜尋算法應用的重要領域之一。A*算法基本思想是通過劃分網格,計算起點到當前點的距離G和目標點到當前點的距離H的和,通過比較大小,把可能通過的點儲存進open列表,而不會考慮的點則儲存進closed列表。
1.3 粒子群算法(ACO)
粒子群算法(PSO)是一種群智能算法,其基本思想是模擬鳥群覓食的行為,通過鳥類之間的集體協作使群體飛行路線最優的算法[4]。在粒子群算法中,用無質量無體積的粒子作個體,并且為每個粒子規定一定的運動規則,從而使整個群體表現出一定的復雜特性。PSO概念簡明,無需復雜的調整、收斂速度快,收斂準確、設置參數少、實現簡單,且其數學基礎相對薄弱,沒有系統的數學基礎。
1.4 矩陣實驗室(MATLAB)
MATLAB是適用于數值計算、數據分析及可視化、算法開發等場合的高級技術計算語言,具有矩陣運算、繪制函數、數據圖像等功能,本研究即在交互式環境中對算法進行編程,進行特定算法計算,實現動態仿真和數據輸出。
2 路徑規劃算法原理
2.1 人工勢場法原理
2.1.1 人工勢場法函數
經典勢能函數將運動物體(汽車)作為一個運動質點置于虛擬人工勢場之中:運動終點與汽車相互作用產生的引力場用式(1)表示,障礙物與汽車相互作用產生的斥力場用式(2)表示[5-10],即:

輸入初始條件、汽車信息等參數,實時采集并更新車道環境參數,建立動態勢場分布,在虛擬力的作用下完成路徑規劃。
2.1.2 人工勢場法程序設計及仿真結果
基于人工市場法在MATLAB環境進行設計。
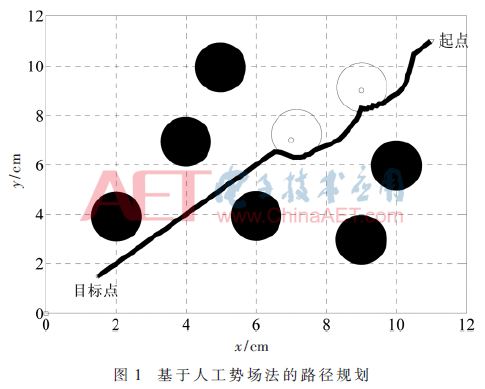
初始條件為:起始點為(10.5,10.5),終點(1.5,1.5)。系統參數為:引力的增益系數k=20;斥力增益系數m=20;障礙影響距離P=1;障礙個數n=8;步長a=0.5;l=0.4;循環迭代次數j=200。
基于人工勢場法設計的路徑規劃如圖1,障礙物為實心圓圈,空心圓圈代表障礙物的大小是障礙物半徑和障礙物的斥力之和,因此路徑會進入障礙物范圍;將信息數據輸入式(1)、式(2)運算行車終點引力和障礙斥力總和,獲得安全避障行駛的相關數據。
2.2 A*搜尋算法(a星算法)
路徑優化的第一步是把地圖簡化成容易控制的搜索形式,即通過劃分網格,把本文的地圖劃分為10×10的小網格。
2.2.1 A*算法的相關參數
(1)Open列表和Closed列表
①一個記錄下所有被考慮來尋找最短路徑方塊的列表,被稱為OPEN列表。
②一個記錄下所有不會再考慮來尋找最短路徑方塊的列表,其中包括起點和邊界,被稱為Closed列表。
(2)路徑增量
G值是從開始點到當前點所在的方塊的移動量,即規定從開始點到相鄰方塊的移動量為1,其值會隨著距離開始點越來越遠而增大。
H值是從當前點靠目標點的移動量的估計值,在算法中常被稱為探視,而估計值越接近真實值,最終的路線會更加精確。如果估計值停止作用,則規劃的路徑很大概率不是最短,通常使用的是“曼哈頓距離方法”,其僅僅是計算出當前點距離目標點剩下的方塊總數,除去障礙物的總數。
2.2.2 A*搜尋算法的規劃流程
(1)將地圖劃分為n×n的網格;
(2)計算G+H的和F;
(3)將方塊提價到open列表中,本列表中有最小的F值,將此值稱為S。
(4)將S從open列表中移除,添加到closed列表中;
(5)對于與S相鄰的四周方塊T可進行如下運算:
①如果T在closed列表中,刪除,不考慮;
②如果T不在open列表中,計算其和值并添加進open列表中;
③如果T在open列表中,當使用當前生成的路徑到達T時,檢查F值是否更小,如果是,更新和值F并前進[11-12]。
2.2.3 A*星算法程序設計及仿真結果
基于A*星搜索算法在MATLAB中進行路徑仿真,結果如圖2,其中障礙物的布置同人工勢場法,邊界的限定為[1,11]。
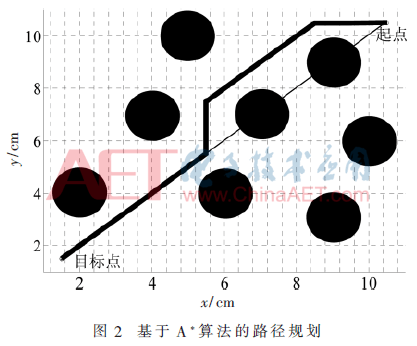
如圖2,其中黑色粗線條代表從起點到終點的直線距離,之后用于比較規劃路徑距離的長短,細線條為A*算法的實際路徑。
2.3 粒子群算法(PSO算法)
2.3.1 粒子群算法參數的選取
粒子群算法主要確定如下各項參數[13-14]:
(1)粒子數目:粒子數越大,則粒子的搜索的空間范圍越大,但相應的搜索所需時間也越大。一般的粒子數取20~40,由于本文的問題比較特殊,本文的粒子數目取200。
(2)粒子長度:大小決定于具體問題。
(3)粒子范圍:大小取決于具體優化問題,且粒子的每一維度可設置不同的取值范圍。
(4)粒子最大速率:大小決定了粒子在一次運行中可以移動的最大距離,如果不限定粒子的極限速率,粒子可能會在一次運行中超出搜索空間,而粒子最大速率的設定取決于粒子范圍的最大寬度。
(5)學習因子(加速常數):固定常數,一般取2。當沒有慣性權重時,引入收斂因子,其取值也不一定取2,C1+C2=4.1時,收斂因子取0.729。部分實驗研究表明兩個因子相等且都等于0.2時效果更好,部分實驗也表明C1大于C2且其和小于4時效果更好。
(6)算法終止條件:最大的迭代次數和在一定的誤差范圍內都可作為終止條件。
(7)適應度函數:目標函數或目標函數的變換。
2.3.2 粒子群算法的具體步驟
算法的流程可以描述如下:
(1)初始化一群粒子(種群規模為M),其中包括隨機位置X和隨機速度V;通常是在范圍內隨機產生。設定學習因子C1、C2,最大迭代次數Gmax。
(2)評價每個粒子的適應度;
(3)對每個粒子的適應值和其經過的歷史最好位置Pbest作對比,如果較好,則選擇其作為當前最優位置,即更新個體極值。
(4)對每個粒子的適應值和種群經過的歷史最好位置Gbest作對比,如果較好,則選擇其作為當前最優位置,即更新全局極值。
(5)根據式(1)、式(2)對粒子位置和速度進行更新,產生新的種群。
(6)如果迭代次數達到終止條件,則停止迭代,算法終止;未達到約束條件時轉到步驟(2),且粒子數加1。
根據上述步驟得出如圖3所示流程圖[15-16]。
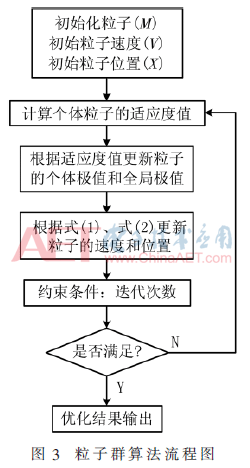
2.3.3 仿真結果
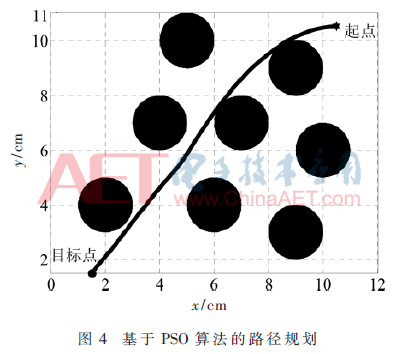
基于PSO算法在MATLAB中進行路徑仿真,結果如圖4,其中障礙物的布置同人工勢場法,邊界的限定為[1,11]。
3 3種算法的特性對比
通過tic和t=toc得出算法運行時間,通過對坐標進行統計運算計算出距離的大小,結果如表1。

從表中可得出如下結論:
(1)地圖相同的前提下,粒子群算法由于需要進行多次迭代,因此所用的時間相對于其他兩種算法很大,而由其得到的路徑非最短路徑。
(2)地圖相同的前提下,A*搜索算法僅進行其局部范圍的最優規劃,因此得出的路徑不是最短,而其時間相對于粒子群算法也小很多。
(3)人工勢場法在路徑長短和時間上最優。
4 粒子群算法的改進
由于粒子群算法是群智能算法的一種,相對于其他兩種算法雖然存在一定缺陷,但也是未來智能行業的一大支點,因此作為一種智能算法,提升空間很大。本文通過一種改進方法來提升粒子群算法的仿真時間,同時優化其路徑。
通過對其各個程序的調用發現,仿真時間與粒子群算法自身處理程序有關,仿真時間占所有時間的15%,仿真時間主要是在調用算法的過程中,因此需要對算法參數進行改進。
采用中期隨機的慣性權重,把w分為分段函數的判斷形式進行粒子全局尋優,彌補了傳統的后期隨機的慣性權重的缺陷。提出在搜索中期采用(0.2,0.8)均勻分布的隨機慣性權重,使用中期隨機的慣性權重。
當it<0.2·MaxIt時,慣性權重取值:

式中,MaxIt為最大迭代次數,It為當前迭代次數,wmax=0.9為最大慣性權重,wmin=0.4為最小慣性權重。
中期隨機的慣性權重具有一定優勢,當前期搜索不到最優解時,在搜索中期時不至于陷入局部最優,因此減弱粒子群算法對迭代次數的依賴,弱化了最大迭代次數對算法的過度依賴。當最大迭代次數過大或過小時,對算法的早熟收斂和最優解的準確度的影響減弱。改善粒子群慣性權重的選擇方式,減少搜索中期出現的過早收斂或者陷入早熟的陷阱中。因此中期隨機即保證了隨機搜索的能力,又保證了收斂速度。
決定粒子群算法的參數還有學習因子C1、C2,粒子群在搜索過程中,需要前段速度大,防止其過早成熟而陷入局部收斂,因此C1取大值,C2取小值。在搜索后期,由于其逐漸向全局最優靠近,因此需要弱化其全局搜索的能力,增強局部搜索的能力,從而減少仿真時間,因此C1取小值,C2取大值。
其分段公式如下:

其中,x=Itπ/MaxIt。當1≤It≤0.47MaxIt時,C1>C2;當0.47MaxIt≤It≤MaxIt時,C1<C2。
通過對慣性權重和學習因子參數進行改進,仿真時間為119.62 s,規劃路徑長度為12.55 m,在提升仿真時間和路徑上有一定的效果。通過雙重參數的調節,保證局部搜索和全局搜索能力的均衡,也保證自身認知和社會認知的均衡化。相比于傳統固定參數和僅僅改變一種參數的結果,本仿真效果有很大的改善。
本文通過求Shubert函數的最小值對以上理論進行驗證對比,選擇Shubert函數的原因是由于其具有很多局部最優解,這里把多元多峰函數變成單元多峰函數進行其最小值的求解,通過此函數得出最小值的驗證更能證明改進后的粒子群算法的效果,其具體數據如表2所示。從表中可看出,經過兩種參數改進后的粒子群算法在收斂到極小值時的收斂速度更快、更準確。

5 結論
自動規劃路徑的核心是選取最優算法,在復雜地圖中,智能算法不一定比普通搜索算法強,而是要通過具體的地圖進行判斷。當然智能算法是人類科技發展的方向,通過對其各項參數進行改進后得出的路徑長度有了很大的提高,其路徑通過不斷迭代得出的結果非常理想。其他智能算法,如遺傳算法[17]、蟻群算法[18]等也各具特性。
參考文獻
[1] 吳初娜.駕駛人應激反應能力評估研究[D].西安:長安大學,2011:30-40.
[2] 胡愛軍,王朝暉.汽車主動安全技術[J].機械設計與制造,2010,48(7):97-99.
[3] 季榮濤,周獻中,王慧平,等.基于Lyapunov法和勢場法的對峙跟蹤研究[J].火力與指揮控制,2016,54(4):66-69.
[4] 許源.結合粒子群算法和改進人工勢場法的移動機器人混合路徑規劃[D].杭州:浙江大學,2013.
[5] 錢森,訾斌.多起重協作吊裝避障路徑規劃研究[J].機械設計與制造,2015(10):260-263.
[6] 祝雪芬,涂剛毅.基于軌跡安全性評價的免疫遺傳路徑規劃算法[J].計算機應用研究,2013,30(2):354-356.
[7] 何海洋.工業機器人無碰軌跡規劃算法研究[D].廣州:華南理工大學,2014.
[8] 楊龍祥.基于反應式的人工勢場發機器人路徑規劃[D].成都:西華大學,2014.
[9] 張煌輝.基于動態人工勢場的路徑規劃研究與應用[D].長沙:長沙理工大學,2010.
[10] 劉秀松.車輛避障駕駛控制方法研究[J].計算機工程與應用,2012,48(2):230-234.
[11] 鄧順平,張艷軍,劉會平.一種基于威脅勢場的A星路徑規劃算法[J].科技視界,2014,4(3):6,22.
[12] 郭強.基于改進的A星算法和B樣條函數的仿生機器魚路徑規劃研究[D].天津:天津大學,2012.
[13] 張萬緒,張向蘭,李瑩.基于改進粒子群算法的智能機器人路徑規劃[J].計算機應用,2014,34(2):510-513.
[14] 吳斌.車輛路徑問題的粒子群算法研究與應用[D].杭州:浙江工業大學,2008.
[15] 劉關俊.基于粒子群算法的移動機器人路徑規劃研究[D].長沙:中南大學,2007.
[16] 王亞春.移動機器人路徑規劃算法研究[D].天津:天津理工大學,2015.
[17] 禹建麗,成元洋之,Valeri.Kroumov.無人駕駛農用運輸車路徑規劃研究[J].拖拉機與農用運輸車,2002,29(4):22-24.
[18] 卜新蘋,蘇虎,鄒偉,等.基于復雜環境非均勻建模的蟻群路徑規劃[J].機器人,2016,38(3):276-284.

