馮亮

　　（浙江師范大學 數理與信息工程學院，浙江 金華 321004）

        摘要：結合深度學習相關理論，提出了海雜波背景下小目標檢測的深度信念網絡方法。該方法以無標簽數據逐層進行非監督貪婪訓練，使每層得到一個合適的初始值；構建深度信念網絡初步模型，并以帶標簽的數據對該種模型以誤差反向算法對整個網絡的參數進行調優，建立預測模型；最后利用該種預測模型檢測湮沒在海雜波背景下的小目標信號。以加拿大McMaster實測的IPIX雷達數據進行實驗，利用均方根誤差評價性能。實驗結果表明，針對第54#海雜波數據，文章提出的深度信念網絡方法所預測的均方根誤差為0.016，與已有的選擇性支持向量機集成方法均方根誤差0.026 4和K均值有效極限學習機所得的均方根誤差0.042 8相比，預測精度有所提高。

　　關鍵詞：深度信念網絡；海雜波；小目標檢測

　　中圖分類號：TP393.1文獻標識碼：ADOI： 10.19358/j.issn.1674-7720.2017.07.016

　　引用格式：馮亮.海雜波背景下小目標檢測的深度信念網絡方法［J］.微型機與應用，2017,36（7）：53-55，66.

　　0引言

　　海雜波［1］通常是指海洋表面的雷達后向散射回波，具有混沌特性［2］，利用該特性能有效檢測雷達回波是否含有目標信號。海雜波背景下小目標檢測對提高海面監測水平有重大意義。1995年，Haykin和Li［3］結合混沌背景的先驗知識，利用神經網絡構建了非線性預測模型，從預測誤差中檢測到了目標信號;2003年，LopezRisueno等［4］提出了一種基于卷積神經網絡的高復雜度和非平穩雜波環境下的目標檢測算法；2008年，CarreteroMoya等［5］提出了一種海雜波背景下基于radon變換的小目標檢測方法。在國內，文獻［6］基于經驗模態分解理論, 提出了一種基于粒子群算法的支持向量機預測方法，從海雜波中檢測出具有諧波特性的微弱信號;文獻［7］提出了一種基于分形布朗運動模型的S波段雷達海雜波分形維數提取方法；文獻［8］基于在復雜混沌噪聲背景中快速準確提取有用信號，提出基于復雜非線性系統相空間重構理論，采用改進極限學習機(ELM)預測單步誤差檢測微弱信號的方法；文獻［9］基于復雜非線性系統相空間重構理論, 提出了一種混沌背景中微弱信號檢測的選擇性支持向量機集成的方法。

1深度信念網絡原理

　　深度信念網絡（Deep Belief Nets，DBN）［10］是2006年Hinton提出的一種由多層受限玻爾茨曼機（Restricted Boltzmann Machine，RBM）單元概率生成模型，其參數通過預訓練和微調訓練兩個過程來確定。DBN由多個RBM堆疊而成，兩層RBM組成的DBN模型結構如圖1所示。

　　DBN中的RBM是一種由可視層v和隱含層h兩部分神經元構成的神經網絡，每層有若干節點，層內的節點之間沒有連接，v與h之間的權值生成采用非監督貪婪逐層方法。RBM在訓練過程中，可視單元向量值映射給隱層單元，然后隱層單元重構可視單元，重構后的可視單元再次映射給隱層單元，繼而獲得新的隱層單元。假設v有n個可視單元，h有m個隱層單元，則v和h的聯合組態能量函數定義為:

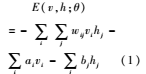
　　其中，vi表示第i個可視單元的狀態，hj表示第j個隱層單元的狀態；θ=(wij,ai,bj)是RBM模型中的3個參數：wij表示可視層節點i與隱含層節點j之間的連接權重，ai表示可視單元i的偏置，bj表示隱層單元j的偏置。基于能量函數，可以得到(v,h)的聯合概率分布：

　　其中，RBM的分配函數為Z(θ)=∑v,he－E(v,h|θ)，條件概率分布為：

　　其中，σ(x)=11+exp(－x)為Sigmoid激活函數。

　　RBM訓練的目的在于求出參數θ=(w,a,b)的值，以此來擬合給定的訓練數據。假設樣本數目為T，參數θ可以通過最大化參數似然函數得到，即:

　　采用Hinton提出的對比散度（Contrastive Divergence，CD）算法，可求得各參數的更新準則：

　　Δwij=η(〈vihj〉data－〈vihj〉recon)(6)

　　Δai=η(〈vi〉data－〈vi〉recon)(7)

　　Δbj=η(〈hj〉data－〈hj〉recon)(8)

　　其中，η為預訓練的學習率，〈·〉data為訓練數據集所定義的分布上的數學期望，〈·〉rencon為重構后模型所定義的分布上的期望。

　　訓練RBM的CD算法步驟如下：

　　（1）初始化可視層單元，可視單元數為n，隱層單元數為m。令v0=x0，w、a、b為服從高斯分布的隨機較小數值，學習率為η，設最大迭代次數為K。

　　（2）計算P(h0j=1|v0)=σ(bj+∑ni=1v0iwij)，從條件分布P(h0j|v0)中提取h0~P(h0|v0)，其中，σ(x)為Sigmoid激活函數。

　　（3）計算P(v1i=1|h0)=σ(ai+∑mi=1h0jwij)，從條件分布P(v1i|h0)中提取v1~P(v1|h0)。

　　（4）計算P(h1j=1|v0)=σ(bj+∑ni=1v1iwij)所有隱層單元。

　　（5）按如下規則更新參數：

　　w←w+η(P(h0=1|v0)vT0-P(h1=1|v1)vT1)

　　a←a+η(v0－v1)

　　b←b+η(P(h0=1|v0)－P(h1=1|v1))

　　（6）重復步驟（2）~（5），直到達到最大迭代次數K，該層RBM訓練完成。

　　非監督的預訓練完成之后，每層RBM可以調整到一個合適的初始值，然后通過自底向上組合多個RBM，可以構建一個DBN初步框架，接下來利用BP算法對整個網絡有監督地進行調優，進一步優化網絡各層的參數，使網絡性能更優。

　　值得注意的是，在DBN的調優過程中，利用RBM的權值初始化BP神經網絡各層的權值，而不像傳統神經網絡隨機初始化。

　　總之，DBN的建立過程可簡單地歸納為兩步：

　　（1）非監督貪婪逐層訓練：基于對比散度CD算法，依據求得的參數更新準則，依照能量最小逐層訓練每個RBM，獲取可視層與隱含層之間的連接權值。

　　（2）有監督微調：基于第一步RBM訓練之后，DBN模型利用帶標簽的數據誤差反向傳播算法（BP）對整個網絡的參數進行調優。

　　2DBN小目標檢測

　　為了驗證本文提出的DBN檢測方法的有效性，對海雜波數據進行建模預測，研究DBN模在海雜波背景下小目標檢測的精度，利用均方根誤差作為評價指標。

　　本文采用的海雜波數據是加拿大McMaster大學的IPIX雷達實測海雜波數據。該雷達發射頻率為9.39 GHz，天線高度30 m，極化方式分為HH、VV、HV 和VH，每個回波數據包含131 072個采樣點，共包含16個距離單元，天線增益為45.7 dB。本文采用的是雷達數據集的第17#及54#海雜波數據。其中分別選取17#海雜波的第一距離單元（不含目標）和第九距離單元（含目標），數據采樣VV極化方式的2 500個點，前1 700個采樣點作為訓練樣本，后800個作為驗證集。同樣，分別選取54#海雜波的第一距離單元（不含目標）和第八距離單元（含目標），數據采樣VV極化方式的2 500個點，前1 700個采樣點作為訓練樣本，后800個作為驗證集。程序在MATLAB2012b版本上運行。erri為預測值與實際值的偏差，均方根誤差作為評價指標：

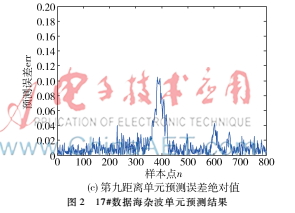
　　設置RBM訓練最大迭代次數為1 000，BP微調時最大迭代次數也為1 000，DBN隱層數量（即RBM層數）為單層，隱層的神經元數量（即隱層節點）為20。建立DBN模型，用DBN進行單步預測，經計算17#第一距離單元的RMSE為0.012 4，第九距離單元RMSE為0.022 1。如圖2所示。比較圖2(b)和(c)，第九距離單元（含目標）的預測誤差中存在明顯尖峰，而第一距離單元（不含目標）的預測誤差則相對光滑。則可以證明DBN模型能檢測湮沒在海雜波背景下的小目標信號。

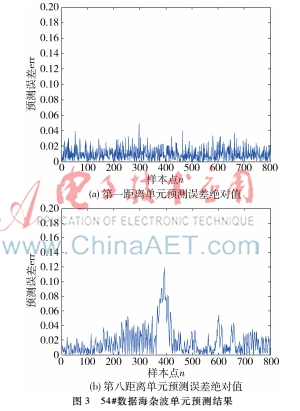
　　同理，選取54#海雜波的第一距離單元和第八距離單元數據再次進行驗證，得到第一距離單元的RMSE為0.012 4，第八距離單元的RMSE為0.025 9，如圖3所示。且從圖3(b)中可直觀地發現預測誤差出現明顯峰值。兩組數據實驗，將目標信號與不含目標信號的距離單元進行對比，都能從圖中看出預測誤差出現明顯的峰值，這說明DBN模型能夠有效地檢測出湮沒在海雜波中的小目標信號。

　　上述實驗RBM層數為單層，隱層節點為20，接下來討論RBM層數和隱層節點對檢測結果的影響，RMSE均方根誤差作為評價指標。從表1可以看出，當RBM層數逐步增加時，DBN模型的預測精度逐步減小；當隱層節點為20，隱層數量為1層時，17#數據集和54#數據集的預測精度最高，即更容易在海雜波背景中檢測出目標信號；而DBN模型在RBM層數多于2層時，其預測誤差的精度則大大降低。 

　　較之傳統神經網絡方法，DBN模型預測方法克服了傳統BP算法需要大量含標簽的訓練集樣本、收斂速度慢、容易陷入局部最優等缺陷，DBN模型能檢測出湮沒在海雜波背景下的小目標信號。與文獻［8］中所提到的有效K均值有效極限學習機所得的RMSE相比，其選取的第54#的第八距離單元的RMSE為0.042 8，本文所提出的DBN方法所得結果優于該方法，均能有效地提高預測的精度；與文獻［9］中所提到的選擇性支持向量機集成的方法相比，其54#的第八距離單元的RMSE為0.026 4，本文所提出的DBN方法預測的RMSE相差不大。

3結論

　　本文利用海雜波的混沌特性，結合深度學習相關理論，提出了在海雜波背景下的小目標檢測方法，用DBN模型檢測出湮沒在海雜波背景下的小目標信號。在海雜波背景下，DBN模型能有效地檢測到小目標信號，與文獻［8］、［9］所述方法相比，DBN模型的檢測效果更好，有更低的預測誤差。

　　參考文獻

　　［1］ 行鴻彥, 朱清清, 徐偉. 一種混沌海雜波背景下的微弱信號檢測方法［J］. 物理學報, 2014, 63(10):41-47.

　　［2］ 朱艷平. 各種混沌系統性能比較研究［J］. 微型機與應用, 2016, 35(12):46.

　　［3］ HAYKIN S, LI X B. Detection of signals in chaos［J］. Proceedings of the IEEE, 1995, 83(1):95-122.

　　［4］ LOPEZRISUENO G, GRAJAL J, DIAZOLIVER R. Target detection in sea clutter using convolutional neural networks［C］. Proceedings of the Radar Conference, 2003. IEEE, 2003:321-328.

　　［5］ CARRETEROMOYA J, GISMEROMENOYO J, ASENSIOLOPEZ A, et al. Smalltarget detection in sea clutter based on the radon transform［C］. International Conference on Radar, 2008:610-615.

　　［6］ 行鴻彥, 張強, 徐偉. 混沌海雜波背景下的微弱信號檢測混合算法［J］. 物理學報, 2015,64(4):48-54.

　　［7］ 姜斌, 王宏強, 黎湘,等. 海雜波背景下的目標檢測新方法［J］. 物理學報, 2006, 55(8):3985-3991.

　　［8］ 商慶健, 張金敏, 王廳長. 基于有效K均值有效極限學習機的混沌海雜波背景中微弱信號檢測［J］. 計算機應用, 2015, 35(3):896-900.

　　［9］ 行鴻彥, 祁崢東, 徐偉. 基于選擇性支持向量機集成的海雜波背景中的微弱信號檢測［J］. 物理學報, 2012, 61(24):82-87.

　　［10］ HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets.［J］. Neural Computation, 2006, 18(7):1527-1554.