劉帥，王平，邢建春，張孝鵬

　　(解放軍理工大學 國防工程學院,江蘇 南京 210007)

        摘要：分析了對稱加密算法AES和非對稱加密算法ECC的加密過程和特點，并結合兩種算法的特點設計了一種混合的加密體制，在避免了對稱加密算法復雜的密鑰分配體制的同時保證了加密的效率和強度。同時引入了改進的數字簽名算法，在對信息來源的真實性和完整性進行驗證的同時，避免了復雜的模逆運算，提高了運算效率。

　　關鍵詞：混合加密；高級加密標準；橢圓曲線密碼；數字簽名

0引言

　　隨著計算機運算能力的不斷增強，各種破解密碼技術層出不窮，傳統的加密技術不斷遭到挑戰。此外，對信息來源的真實性以及完整性的驗證也越來越受到重視。當今應用最廣泛的兩種密碼體制有著各自不同的優點和缺陷；對稱密碼體制加解密速度快，但是密鑰分配與管理比較復雜；非對稱密碼體制可以進行數字簽名且密鑰管理比較方便，但是加解密速度比較慢，運算量比較大。如何利用兩者優點的同時盡可能地避免各自的缺陷，以達到更好的加密效果，是近年來的研究熱點。本文結合對稱加密中的高級加密標準［1］(AES)和非對稱加密中的橢圓曲線密碼體制［2］(ECC)兩者的特點，在對傳統簽名算法改進的基礎上設計了一種混合加密方案，具有安全性高、加解密速度快等優點。

1AES加密算法

　　AES算法是一種數據分組長度為128 bit的迭代分組加密算法，根據加密級別的不同，其密鑰長度有128 bit、192 bit和256 bit 3種選擇，對應的迭代循環次數分別為10輪、12輪和14輪。每一輪變換由4個部分組成，分別是字節替換(SubBytes)、行位移(ShiftRows)、列混合(MixColumns)和輪密鑰加(AddRoundKey)［3］，其中最后一輪沒有列混合的操作。以密鑰長度128 bit為例，AES算法的加密過程如圖1所示。

　　因為AES算法加密屬于對稱加密體制，加密和解密的過程中通信雙方使用相同的密鑰，所以解密過程與加密過程基本相同，只是密鑰的使用順序正好相反，所以對于解密過程在此不再贅述。

　　對稱加密算法AES具有速度快、強度高、安全性好、便于實現等優點［4］。但是對稱性的加密體制也為其帶來了一些缺陷，主要包括以下兩個方面：首先是系統中任意兩個節點之間的通信都需要一對獨立的密鑰，所以在系統內每增加一個通信節點密鑰量便會成倍增加，由此帶來的密鑰產生、存放和分配的問題無疑是極其繁重的；其次是密鑰的傳輸問題，在對稱密碼體制中由于通信雙方使用的是相同的密鑰，加密的安全性也完全依賴于對密鑰的保護，一旦密鑰在傳輸過程中被竊取，加密便變得沒有意義。為了解決這一問題，必須使用一些特殊的安全信道來分發密鑰，譬如用專門信使來傳送密鑰，而這一做法的代價是相當大的，甚至可以說是不現實的。

2ECC加密算法

　　2.1ECC算法的描述

　　ECC算法是KOBLITZ N和MILLER在1985年提出的一種非對稱加密算法，它對數據加密的安全性是基于橢圓曲線離散對數問題求解的困難性。這里所講的橢圓曲線指的是韋爾斯特拉斯（Weierstrass）方程所確定的平面曲線，即：

　　y2+a1xy+a3y=x3+a2x2+a4x+a6

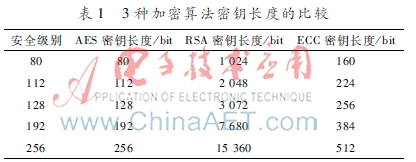
　　其中,系數ai(i=1,2,…,6)定義在某個域上，可以是有理數域、實數域、復數域，也可以是有限域GF（pr），橢圓曲線密碼體制中用到的橢圓曲線都是定義在有限域上的。橢圓曲線上所有的點，外加一個叫做無窮遠點的特殊點構成的集合，連同一個定義的加法運算構成一個Abel群［5］。在等式P+P+…+P=dP=T中，已知d和點P求點T比較容易，反之已知點T和點P求d卻是相當困難的，這個問題稱為橢圓曲線上點群的離散對數問題［6］。從表1不難看出，ECC算法用較小的密鑰長度即可達到與RSA算法相同的加密強度，與其他非對稱加密算法相比ECC算法具有安全性更高、密鑰短、需要存儲空間比較小等優勢［7］。至今人們尚未找到有限域上橢圓曲線有理點群的離散對數問題的亞指數算法，而且目前的研究結果表明構造出這樣的亞指數算法的可能性不大［8］。

　　2.2數字簽名

　　傳統的數字簽名算法在簽名過程中要進行模逆運算，求逆運算的復雜性是造成簽名速度慢的主要原因。因此構造一個新的簽名方程，使得改進后的簽名算法不用進行模的逆運算，以達到提高效率的目的［9］。

　　2.2.1改進后的簽名及驗證過程

　　(1)發送方選擇隨機數k，使得k∈［1,n+1］；

　　(2)發送方用SHA1函數處理將要發送的明文m，生成摘要；

　　(3)發送方向接收方傳送選擇好的函數和確定的相關參數；

　　(4)發送方選擇密鑰x，并用公開基點g計算y=xg，得到公鑰y；

　　(5)計算r=kg,若r=0則轉到步驟(1)；

　　(6)計算s=k-mrx,得到(s,r)作為簽名；

　　(7)將簽名(s,r)連同明文m發送給接收方；

　　(8)接收方計算r′=sg+mry；

　　(9)接收方判定r=r′是否成立，若成立則簽名成立，若不成立則簽名無效。

　　2.2.2無需模逆運算的證明

　　簽名過程的計算公式：

　　s=k-mrx

　　驗證過程的計算公式：

　　r′=sg+mry

　　證明：

　　將y=xg和s=k-mrx帶入驗證公式：

　　r′=sg+mry=(k-mrx)g+mr(xg)=kg-mrxg+mrxg=kg=r

　　此方案不需要進行模擬操作，減輕了運算的負擔，提高了運算速度，對系統的效能要求更低， 更具有實用意義［9］。

　　公鑰加密算法在加解密過程中使用的密鑰是不同的，加密過程的密鑰是對外公開的，稱為公鑰；但解密過程的密鑰只有接收信息的一方知道，稱為私鑰。兩個密鑰是相對獨立的。這一特點避免了對稱加密算法繁雜的密鑰分配體制，所以非對稱密碼體制的優點在于密鑰的分配和管理相對簡單。此外，公鑰加密算法可以通過對要傳送的信息進行數字簽名的方式，對信息來源的真實性以及完整性進行驗證。雖然已對簽名算法進行了相應改進，但是較對稱密碼體制而言其算法依舊非常復雜、加解密的效率低，使得對實時性要求比較高、信息量比較大的系統實現起來比較困難。

3混合加密體制的設計與實現方案

　　3.1發送端的設計

　　發送端的設計主要分為以下3個部分：

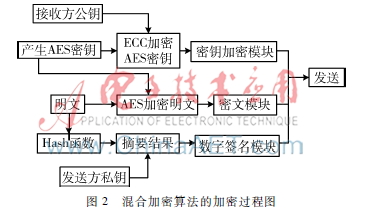
　　(1)密鑰加密模塊：在加密開始前會隨機產生AES的加密密鑰，為避免AES算法繁重的密鑰分配和管理工作，接收方以掌握的接收方分享的公鑰用ECC算法來對AES的密鑰進行加密，生成“密鑰加密模塊”。

　　(2)密文模塊：AES算法對明文進行加密，生成“密文模塊”。

　　(3)數字簽名模塊：用Hash函數對需要發送的明文進行處理生成摘要結果，發送方用自己的私鑰對摘要結果進行加密生成“數字簽名模塊”。

　　將生成的3個模塊組合發送給接收方，發送端任務完畢。圖2為混合加密算法的加密過程圖。

　　3.2接收端的設計

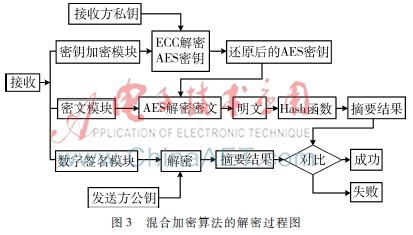
　　接收端在接收到組合的加密信息后，對3個模塊分別進行處理：

　　(1)密鑰加密模塊：接收方以自己掌握的私鑰對ECC加密的密鑰加密模塊進行解密，得到AES算法的加密密鑰。

　　(2)密文模塊：用解密后AES算法的密鑰對密文模塊進行解密，得到明文。對解密后的明文進行Hash函數處理得到摘要結果。

　　(3)數字簽名模塊：接收方用發送方分享的公鑰對數字簽名模塊進行解密，解密后得到發送方發過來的摘要結果。將解密得到的密文處理后的正確的摘要結果與發送方生成的摘要結果進行對比，以此來進行身份驗證。如果相同則身份驗證成功，不相同則身份驗證失敗。

　　若身份驗證成功則解密得到的明文可用，若身份驗證失敗則說明信息很有可能已被篡改，需重新發送。圖3為混合加密算法的解密過程圖。

4結論

　　改進的混合加密算法對相對大量的明文主體數據采用了安全性非常高、速度非常快的AES算法［10］，對于AES算法的密鑰則使用ECC算法進行加密，在保證密鑰安全的同時有效避免了對稱加密算法密鑰的單獨發送，極大地提高了加密的效率，保證了密鑰的安全。此外，數字簽名功能的引入，可以對信息的來源和信息的完整性進行驗證，從而進一步保證了通信安全。在對簽名算法進行改進和優化之后，避免了模逆運算，節省了數字簽名的時間，進一步提升了加密效率。

　　該方案加密等級高、速度快，特別是對通信實時性、安全性要求比較高的領域，該方案的實用性較強。

　　參考文獻

　　［1］ PETHE H B, PANDE S R. A survey on different secret key cryptographic algorithms［J］. Ibmrds Journal of Management & Research, 2014, 3(1)：142150.

　　［2］ Zhang Haibin, Ji Xiaoping, Wu Boying, et al. Fast elliptic curve point multiplication algorithm optimization［J］. Applied Mechanics and Materials, 2014, 441: 10441048.

　　［3］ 張慧霞,趙建平,李曉麗,等. AES密碼算法的FPGA實現與仿真 ［J］. 通信技術,2013,46(9):8385.

　　［4］ 馬擎宇,張東. 基于AES和ECC的遙測數據加密技術研究與實現 ［J］. 艦船電子工程,2015,35(4):7881.

　　［5］ 江志祥,藺志青. 橢圓曲線密碼體制［EB/OL］. （20080102）［20151210］.//www.paper.edu.cn/html/releasepaper/2008/01/21.

　　［6］ PAAR C, PELZL J. Understanding cryptography: a textbook for students and practitioners ［M］. Berlin: SpringerVerlag,200912.

　　［7］ CRYPTOGRAPHY E C. The advantages of elliptic curve cryptography for wireless security［J］. IEEE Wireless Communications,2004,2:6267.

　　［8］ 寧國強,李謝華,尹張飛.一種安全的即時通信解決方案［J］.計算機工程與應用,2011，47(3)：8283.

　　［9］ 劉軍,賈松浩,楊彩.改進的ECC算法在數字認證中心系統應用［J］.實驗室研究與探索,2014，33(2)：108111.

　　［10］ 劉楠，陳迅，李軍偉.面向CBC模式的AES高速芯片設計與實現［J］. 電子技術應用,2014,40(1):6467.