文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2016.03.011
中文引用格式: 尹培培. 非精確浮點數乘法器設計[J].電子技術應用,2016,42(3):38-41,46.
英文引用格式: Yin Peipei. Design and analysis of inexact floating-point multiplier[J].Application of Electronic Technique,2016,42(3):38-41,46.
0 引言
目前,集成電路的設計工藝已經進入深亞微米階段,工藝水平大幅度提高,計算機微處理器也不斷更新換代。在微處理系統中,數據類型分為定點數和浮點數,相對于定點數的有限范圍及有限精度,浮點數可以靈活地表示更大范圍及更高精度的實數,由于以上原因,浮點數運算成為微處理器以及信號處理系統中的重要部件之一。但同時相對于定點數而言,浮點數運算需要更復雜的硬件電路,消耗更大的面積及能量,因此為數據范圍的拓寬帶來了能量及面積上的消耗。傳統的電路設計大多運用精確計算算法,但對于一些圖像處理的可容錯應用,這些系統并不需要絕對的精確性。所以將非精確運算[1]運用到這些系統中可以減小能量損耗及電路面積,同時也可提高系統的性能。
非精確的算法設計作為減少容錯設備的動態及靜態能量損耗的有效方法,它的主要思想是通過減小硬件的復雜度來提高系統的性能及效率。目前非精確計算主要集中在定點數的研究[2-5],文獻[2]中非精確處理器犧牲了7.58%的相對錯誤率,但速度、面積比精確處理器速度提高了將近15倍,能量損耗也減少了將近15倍。研究表明運用非精確算法設計出的芯片面積更小,速度更快,能量損耗更低。雖然定點數在非精確研究方面取得了較成功的應用,但相對于定點數而言,目前對非精確浮點數運算的研究并不多。由于浮點數運算電路更復雜,能量也消耗更多,非精確浮點數算法的研究顯得尤為重要。
文獻[5]設計了一種非精確的浮點數加法器,該設計通過將低位部分精確加法替代為或門算法實現非精確運算;文獻[6]研究了一種低功耗的浮點數乘法器,該研究通過直接截斷浮點數的數值位來減少硬件;文獻[7]設計了一種高效率的浮點數乘法器;文獻[8]利用低精度浮點數來減小MP3解碼時的內存損耗。
本文提出了一種非精確浮點數乘法器的算法設計,同時將該算法應用于高動態范圍圖片的圖像處理中,并將結果與精確浮點數乘法器的應用結果進行對比。文章內容分布如下:在第1節中,首先簡單介紹了浮點數構成及精確的浮點數乘法器的結構;在第2節中提出了非精確乘法器的設計方法;在第3節中將該非精確乘法器應用到高動態范圍圖片中;最后總結了該設計算法。
1 背景簡介
1.1 浮點數表示方法
在算數運算中,數據的表示方法有兩個,定點數和浮點數。定點數可以表示以0為中心的一定范圍的正負整數,由于定點數小數點固定,不能表示太大動態范圍的數,同時也不能表示過大或過小的數,此時浮點數的優勢就體現了出來,它可以在不增加位數的前提下擴展數據的動態范圍。
在IEEE 754-2008標準中,浮點數是一個以3個量表示的二進制位串(如圖1所示),該位串分為3個部分:符號位部分、指數位部分和尾數位部分。

浮點數的標準表達式為:

其中,S為符號位,當S=0時表示該浮點數是一個正值,當S=1時表示該浮點數是一個負值;E為指數位,bias表示偏移量,對于單精度bias=127,雙精度bias=1023,則E-bias既可為正數也可為負數;M為尾數位,對于規格化的尾數,存儲時默認省去小數點前的1,則對于非零尾數,尾數值為1.M。
1.2 精確浮點數乘法器
最初的浮點數乘法器是依靠軟件實現的,但隨著超大規模集成技術的發展以及乘法器對計算速度要求的提高,乘法運算逐漸變成一個硬件的部件,浮點數乘法的基本原理是將相乘兩數的指數和作為乘積的指數,相乘兩數尾數的積作為乘積的尾數,相乘兩數的符號位異或作為乘積符號位。
精確的浮點數乘法器如圖2所示,默認這里兩個操作數都已規格化,如若沒有,則首先需將輸入的操作數規格化。然后從兩操作數中分別提取每個操作數的符號位、指數位及尾數位,并將尾數位補充省略的第一位1。浮點數的乘法只要包括兩個運算:指數的加法和尾數的乘法,這兩運算結束后就是將結果進行規格化,生成符合IEEE 754-2008標準的結果。

2 非精確浮點數乘法器設計
非精確乘法器的設計是基于圖2所示的精確計算的算法級設計,主要是將非精確定點數乘法器運用到浮點數尾數乘法設計中,同時考慮到尾數乘積已是非精確結果,舍入單元及規格化也進行了簡化。
2.1 尾數乘法器
尾數乘法器就是計算兩個浮點數尾數部分的乘積,也就是兩個無符號定點數的乘法,主要包括3個部分:部分積的生成、部分積壓縮及最終結果的生成。本文部分積通過非精確Booth編碼[9]生成,部分積壓縮通過非精確4-2壓縮器[10]及Wallace樹[11]完成。對于單精度浮點數,尾數的乘法是無符號定點24×24位的乘法器,修正Booth編碼產生了13個部分積;4-2壓縮器、Wallace樹以及進位存儲加法器將部分積壓縮成2個操作數;最后48位和進位采用快速超前進位加法器相加。
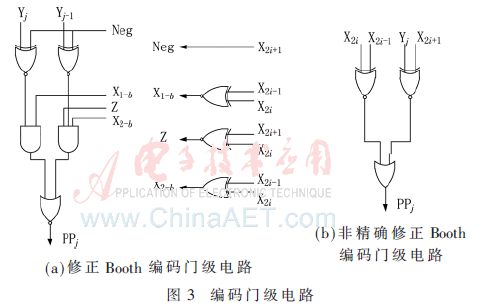
非精確Booth編碼是在修正Booth編碼算法上改進的,修正Booth編碼算法的門級電路如圖3(a)所示,式(2)給出了部分積(Partial Products,PP)與輸入之間的關系。非精確Booth編碼的門級電路如圖3(b)所示,式(3)給出了部分積與輸入之間的關系。

部分積的壓縮通過4-2壓縮器實現,非精確壓縮器是在精確4-2壓縮器上改進得到,精確4-2壓縮器的實現方法如圖4(a)所示,式(4)~式(6)給出了壓縮結果與部分積輸入之間的關系。非精確4-2壓縮器的實現方法如圖4(b)所示,式(7)~式(8)給出了壓縮結果與部分積輸入之間的關系。
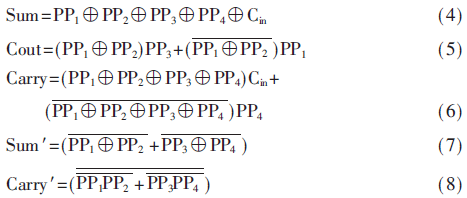
以單精度浮點數為例,非精確尾數乘法器的Wallace樹結構如圖5所示,由于最終標準化后只取乘積的前24位,所以進行24×24乘法時0~23位的計算直接舍去,24~42位進行非精確計算,43~47位進行精確計算,圖5中實線框中進行非精確Booth編碼及非精確壓縮,虛線框進行精確Booth編碼及精確壓縮。

2.2 舍入單元
舍入單元的作用是在結果被返回放回浮點格式時,將多出來的位舍棄,使得有效數據的位數保持在固定的位數范圍內。在精確浮點數乘法器中,IEEE列出了4種不同的舍入方法:舍入到最近(Round To Nearest,RTN)、朝正無窮大方向舍入(Round To Positive Infinity,RTPI)、朝負無窮大方向舍入(Round To Negative Infinity,RTNI)、朝0方向舍入(Round To Zero,RTZ)。在非精確設計中,乘積結果已是非精確的,舍入方法的選擇對算法沒有太大意義,所以在非精確浮點數乘法器中,舍入單元將不再考慮。
2.3 非精確浮點數乘法器結構
基于以上分析,非精確浮點數乘法器可以通過設計非精確無符號定點數乘法器、簡化規格化處理及省略舍入單元來實現,具體結構如圖6所示。

3 圖像處理應用
很多非精確浮點數乘法都應用于圖像處理中, OpenEXR是由Industrial Light and Magic開發的高動態范圍圖片(High Dynamic-Range,HDR)的文件格式,它支持16位及32位浮點。本文采用高動態范圍圖片來驗證該非精確浮點數乘法器的有效性。高動態范圍可視區分度檢測(High Dynamic Range Visible Difference Predictor,HDR-VDP)是度量兩幅圖片區別的方法,它可以檢測兩幅圖片的可視區別。圖7、圖8分別為精確、非精確浮點數乘法生成圖片,兩幅圖片的區別檢測圖如圖9所示。

 HDR-VDP中整體可視檢測中定義了兩個度量方法,一個為P_det,定義為兩幅圖片的可視區別概率,它的范圍為0~1,數值越大,說明兩圖片的區別人眼越容易察覺;另一度量方法是Q_MOS,它定義為圖片的平均觀測質量,它的范圍是0~100,數值越大說明圖片質量越好。經測量本文設計的非精確浮點數乘法器的兩個度量值分別為:
HDR-VDP中整體可視檢測中定義了兩個度量方法,一個為P_det,定義為兩幅圖片的可視區別概率,它的范圍為0~1,數值越大,說明兩圖片的區別人眼越容易察覺;另一度量方法是Q_MOS,它定義為圖片的平均觀測質量,它的范圍是0~100,數值越大說明圖片質量越好。經測量本文設計的非精確浮點數乘法器的兩個度量值分別為:

度量值P_det表明兩幅圖片的差異不太容易被檢測,度量值Q_MOS表明兩幅圖片質量很好。
4 結論
本文主要采用非精確定點尾數乘法器設計非精確浮點數乘法器,并將該乘法器運用到圖像處理中,結果表明本文所設計的非精確浮點數乘法器具有很好的性能。
參考文獻
[1] PALEM K,INGAMNENI A.Ten years of building broken-chips:the physics and engineeringofinexact computing[J].ACMTrans.Embedded Computing Systems,2013,12(2),87:1-23.
[2] LINGAMNENI A,MUNTIMADUGU A,ENZ C,et al.Algorithmic methodologies for ultra-efficient inexact architectures for sustaining technology scaling[J].Proc.ACM Int.Conf.Computing Frontiers,2012:3-12.
[3] YANG Z,JAIN A,LIANG J,et al.Approximate XOR XNOR-based Adders for inexact computing[J].Proc.13rd IEEE Conf.Nanotechnol.(IEEE-NANO),2013:690-693.
[4] Liu Weiqiang,Chen Linbin,Wang Chenghua,et al.Design and analysis of inexact floating-point adders[J].IEEE Transactions on Computers,2016,65(1):308-314.
[5] Liu Weiqiang,Chen Linbin,WANG C,et al.Inexact Floating-Point Adder for Dynamic Image Processing[J].Proceedings of the 14th IEEEInternational Conference on Nano-technology Toronto,Canada,2014.
[6] TONG J Y,NAGLE D,RUTENBAR R.Reducing power byoptimizingthe necessary precision/rangeof floating-point arithmetic[J].IEEE Trans.Very Large Scale Integr.Syst.2000,8:273-286.
[7] GUPTA A,MANDAVALLI S,MOONEY V,et al.Low power probabilistic floatingpoint multiplier design[J].Proc.IEEE Comput.Soc.Annu.Symp.VLSI,2011:182-187.
[8] EILERT J,EHLIAR A,LIU D.Using low precision floating point numbers to reduce memory cost for MP3 decoding[J].Proc. 6th IEEE Workshop on Multimedia Signal Processing,2004:119-122.
[9] YEH W C,JEN C W.High-speed booth encoded parallel multiplier design[J].IEEE Trans.Computers,2000,49(7):692-701.
[10] Amir Momeni,Jie Han,Paolo Montuschi,et al.Design and analysis of approximate compressor for multilication[J].IEEE Trans.Computers,2015,64(4):984-994.
[11] MILLAR B,MADRID P E,SWARTZLANDER E E.A fast hybrid multiplier combining Booth and Wallace/Dadda algorithms[J].Proceedings of the 35th MidwestSymposium on Circuits and Systems,1992,1(8):158-165.

