摘 要: 為克服傳統的低通到高通電路之間轉換的缺陷,從優化設計的低通濾波器的傳輸函數著手,提出了一種通用的從低通到高通變換的新方法。理論與實際都證明了此方法能得到性能良好的高通濾波器。
關鍵詞: 低通濾波器;高通濾波器;傳遞函數
0 引言
濾波器指的是一種能夠使有用頻率信號順利通過,而抑制(或大為衰減)不需要的頻率信號的電子裝置。以往的濾波電路主要由無源元件R、L和C組成,自20世紀60年代以來,隨著集成運放的迅速發展,由它和R、C組成的有源濾波電路相較無源濾波器具有不用電感、體積小、重量輕等優點而得到快速發展,且被廣泛應用于數據傳送、信號處理和抑制干擾等領域。
有源濾波器在人們日常生活中已占有不可或缺的重要地位,常常將其作為一個系統的一個模塊,其性能的好壞,將對整個系統的性能產生決定性的影響。目前國內外對低通濾波器的相關研究已相當成熟[1],但對高通濾波器尤其是高階高通濾波器的研究卻很少。近年來雖有開關電容式專用濾波芯片出現,但其電路噪聲不盡人意。因此開展高階RC有源高通濾波器的優化設計研究具有一定的實用價值。
1 四階高通有源濾波器優化設計步驟
1.1 四階低通濾波器的優化設計
二階低通濾波器既是常用的濾波單元,又是構成高階濾波器的基本組成單位。常見的二階低通濾波電路主要有MFB形式和VCVS形式。由于VCVS形式的二階低通電路具有輸入阻抗很高而輸出阻抗很低、所需的精密電阻與電容器件較少、對運放要求較低等優點,因此本文采用VCVS形式二階濾波節作為組成四階低通的基本單元。典型的二階低通濾波電路如圖1所示。
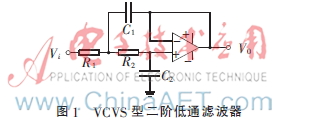
根據基爾霍夫電流定律以及運放的“虛短”、“虛斷”原則,可以推導出圖1的傳輸函數為:
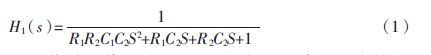
根據線性網絡理論[2],并結合有源濾波器具有輸入與輸出便于級聯而不會產生額外的干擾信號的特點,則四階低通濾波器可由兩個上述二階濾波器的級聯來實現。其電路原理圖如圖2所示。
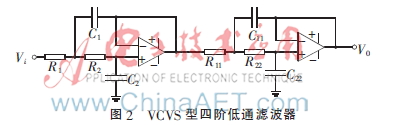
可以推導出其傳輸函數為:
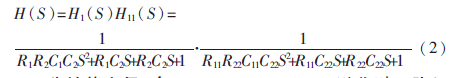
為計算方便,令R1=R2=R11=R22=1 Ω,則此時四階低通的傳輸函數可表示為:
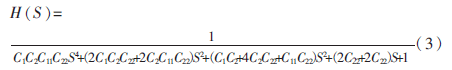
巴特沃斯低通濾波器因在通頻帶內具有大平坦的特點,且在過渡帶與阻帶內具有單調下降的幅頻特性,因而被廣泛應用。四階巴特沃斯歸一化低通傳輸函數[3]可表示為:
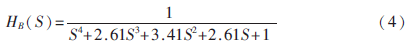
仔細觀察其傳輸函數,不難發現四階巴特沃斯低通傳輸函數可以用上面所述的兩個二階低通傳輸函數網絡的級聯來實現,只要將式(3)與式(4)進行對照,并令它們完全相等,則:
C1C2C11C22=1.00(5)
2C1C2C22+2C2C11C22=2.61(6)
C1C2+4C2C22+C11C22=3.41(7)
2C2+2C22=2.61(8)
從而解得:
C1=1.082,C2=0.924 1,C11=2.613,C22=0.382 5(9)
這樣理論上來講,便把四階低通濾波器優化為了歸一化的四階低通巴特沃斯濾波器。其電路原理如圖3所示。
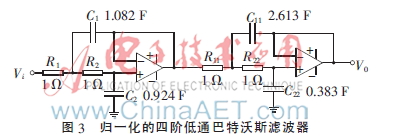
經仿真軟件仿真,此電路確實具有巴特沃斯濾波器的幅頻特性。且此歸一化低通濾波器為接下來高通濾波器的設計奠定了基礎,同時低通濾波器4個電阻的阻值為1,也使得下一步變換成高通濾波器時電容的選擇更加方便快捷。
1.2 四階低通到四階高通的轉換與優化設計
有關低通到高通電路之間的轉換方法,傳統的方法是:將低通網絡中每一個電阻Ri都變換為容量是1/Ri F的電容,同時將每個電容Cj換成阻值為1/Cj ?贅的電阻[4]。這時的高通濾波器的參數變為:
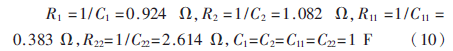
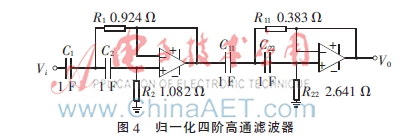
則歸一化四階高通濾波器的電路如圖4所示。
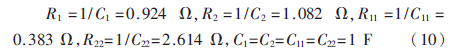
但在實際電路中,這種簡單的從低通到高通的變換通常并不能得到濾波特性較好的高通濾波器。如果仔細觀察分析上述濾波網絡的傳輸函數,如式(1)、式(2),不難發現:若濾波網絡中所有的電阻都乘以一個常數f,而同時所有的電容都除以同一個相同的常數f,則濾波網絡的傳輸函數不變(這是因為電容與電阻總是成對以乘積的形式出現),但其幅頻特性卻能得到大大的改善(通過仿真及實際電路觀測其幅頻特性得到)。
需要注意的是,這個常數的選擇是需要計算的,具體的計算方法見下面的設計實例,同時還需要仿真及調試來最終確定其數值。一般在低頻段其值要大一些,否則反之。
2 設計實例與仿真
2.1 設計要求
設計一高通濾波器,其技術指標為:在600 Hz處最大衰減是3 dB,在250 Hz處的最小衰減為30 dB。
2.2 設計過程
由題意得其轉折頻率ω0=2π×600=3 770 rad/s,先找到歸一化巴特沃斯低通模型,確定濾波器階數。由于600/240=2.5,即它要滿足在2.5 rad/s處的最小衰減為30 dB。通過查找巴特沃斯幅頻響應圖[5],得知四階巴特沃斯低通濾波器滿足要求。
這樣就可以用上述的方法與過程來設計高通濾波器了:在圖3歸一化的四階低通巴特沃斯濾波器的電路基礎上,用前面所說的方法將電容換成電阻,其阻值為該電容的倒數;同時電阻換成電容,其電容值為電阻值的倒數,參數如式(9)所示,得到圖4所示的歸一化高通濾波器。
接下來,如何得到合適的常數f的值呢?為方便起見,先選擇C′=0.1 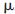 F,則f=C/(C′×ω0)=1/(0.1×10-6×3 770)=2 653,同時通過仿真來驗證,確實當其值為2 653時,具有較好的濾波特性。則此時濾波網絡的參數變為:
F,則f=C/(C′×ω0)=1/(0.1×10-6×3 770)=2 653,同時通過仿真來驗證,確實當其值為2 653時,具有較好的濾波特性。則此時濾波網絡的參數變為:
C1=C2=C11=C22=0.1 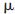 F
F
R1=0.924×2 653=2.45 kΩ
R2=1.082×2 653=2.87 kΩ
R11=0.383×2 653=1.01 kΩ
R22=2.614×2 653=6.93 kΩ
最后電路原理及參數值如圖5所示。
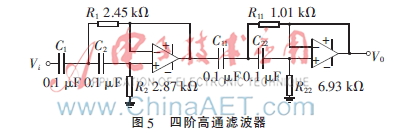
2.3 仿真
本文采用Multisim 11電路仿真軟件,對圖4最后設計出來的帶有參數的四階高通濾波器電路進行仿真。其仿真幅頻特性如圖6所示。高通濾波器歸一化的傳遞函數部分頻點的幅頻特征如表1所示。
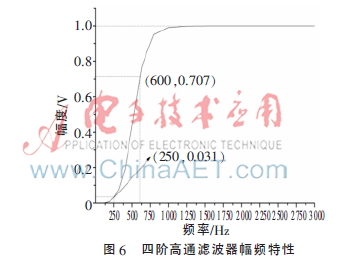

從圖6及表1可以清楚地看到,它在600 Hz處的最大衰減是3 dB,在250 Hz處的最小衰減為30 dB,且在通帶內具有最大幅度的特性,完全滿足設計的要求。
3 結論
本文主要是通過對優化設計的四階巴特沃斯低通濾波器進行從低通到高通的變換,來優化設計四階高通濾波器。事實證明此方法切實可行,能夠滿足設計要求。
參考文獻
[1] 余水寶.高階有源濾波網絡的優化綜合及其應用[J].科技通報,2001,17(2):53-58.
[2] 陳昭炎.高階帶通濾波器的設計[J].嘉應學院學報,2008,25(6):13-18.
[3] 程佩青.數字信號處理教程[M].北京:清華大學出版社,2001.
[4] [美]M.S高西,K.R萊克.現代濾波器設計:有源RC的開關電容[M].北京:科學出版社,1989.
[5] 黃根春,周靖,張望先.全國大學生電子設計競賽教程:基于TI器件設計方法[M].北京:電子工業出版社,2011.

