文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2015.07.041
中文引用格式: 王保坡,杜勁松,田星,等. 基于混合遺傳算法的去耦電容網絡設計[J].電子技術應用,2015,41(7):146-149,153.
英文引用格式: Wang Baopo,Du Jinsong,Tian Xing,et al. Design of decoupling capacitor network based on hybrid GA[J].Application of Electronic Technique,2015,41(7):146-149,153.
0 引言
隨著電子技術的快速發展,電子線路設計的集成度和復雜度越來越高,對PCB設計的電源完整性要求也越來越高。目前針對電源完整性問題的研究方法主要有基于目標阻抗的頻域方法和基于傳輸功率的時域方法。文獻[1]根據目標阻抗和自諧振點對所需電容器種類和數目進行計算和仿真分析[1]。文獻[2]中提出了基于傳輸功率的研究方法[2]。此外還有其他一些方法,比如在去耦支路引入串聯電阻[3]、引入電磁帶隙結構[4]等設計高頻去耦網絡。基于目標阻抗的設計方法已有很多相關論述,而大部分研究的關注點在于容值計算以及去耦特性分析等,較少考慮實際高速高密度PCB設計面臨的布局布線資源有限的問題,因此實用性不強。文獻[5]將遺傳算法應用于去耦電容在PCB上的優化放置[5],通過優化電容器布局增強去耦效果。文獻[6]將遺傳算法應用于PDN設計[6],取得了一定效果。然而標準遺傳算法在處理多極值問題時全局收斂性較差,本文采用改進的遺傳算法對所需去耦電容器的種類和數目進行優化計算,同時與標準遺傳算法和傳統設計方法進行對比,并借助Cadence仿真工具驗證設計結果的有效性和合理性。
1 電容去耦原理及計算方法
電容去耦原理可以通過圖1說明。將圖中的穩壓電源及去耦電容看作一個復合的電源系統,當負載電流變化很快時,穩壓電源不能夠及時響應負載變化,此時電容器充當了局部電源,保證負載電壓穩定。
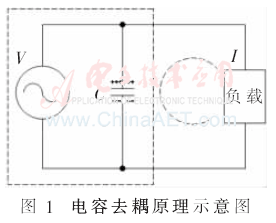
從阻抗角度而言,去耦電容降低了電源系統的交流阻抗,由式(1)可以看出負載電流變化時,Z越小,負載電壓變化量越小,系統電源越穩定。

實際的電容器模型為RLC串聯網絡,當信號頻率小于諧振頻率時呈容性,而在高于諧振頻率時呈感性。其簡化的數學模型由式(2)表示,其中f0為諧振頻率。

傳統的設計方法通常是將目標頻率范圍分段,每個頻段對應一種容值的去耦電容,采用多個不同容值的電容器并聯組成去耦電容網絡,使電源系統滿足目標阻抗要求。圖2顯示了兩種不同容值的電容器C1和C2并聯的頻率響應。
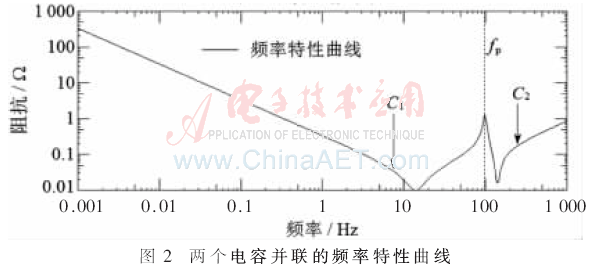
可以看到,在兩個電容的自諧振點之間存在一個阻抗尖峰,該點稱為反諧振點,由于該頻段C1呈現感性,C2呈現容性,實質是LC并聯諧振導致。該點阻抗可以由式(3)估算[7]。

其中s=j2πfp,fp為反諧振頻率。
傳統設計方法通過添加自諧振頻率在反諧振點附近的電容來抑制并聯諧振,但同時又會引入新的反諧振點,因此需要借助仿真軟件反復修改驗證,整個過程較為繁瑣,并且需要憑借一定的設計經驗。
2 基于混合遺傳算法優化設計
由于遺傳算法本身具有較大的隨機性,在針對多峰性質的最優化求解時往往陷入局部極值。本文采用模擬退火與遺傳算法相結合的混合遺傳算法,將項目自行設計的高速PCB作為測試板,針對1.5 V電源進行電容去耦網絡設計。結合分頻段設計思想,將目標頻率范圍進行分段,分別對應一種電容,每種電容器的數目組合構成種群個體。選定的可用電容器種類及參數如表1所示(默認安裝電感均為225 pH)。

首先由隨機函數產生初始種群,對種群個體進行編碼形成染色體。目標函數即為該個體表示的電容器總數目,由式(4)計算得出,其中x(i)為個體所表征的每種電容器數目,N為電容器容值種類。

對種群進行初始化以后,根據特定的適應函數計算個體的適應度(即入選概率),所采用的適應函數和適應度分別由式(5)和式(6)表示。
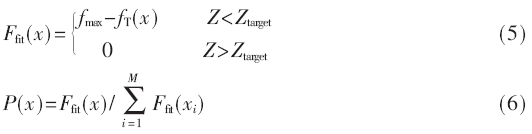
其中M為種群規模。
值得注意的是,式(5)根據個體是否滿足目標阻抗確定相應的適應函數值。下面對具體的驗證策略加以說明,圖3為4種容值的電容器并聯時PDN阻抗示意圖,其中虛線為未添加去耦網絡的阻抗曲線。
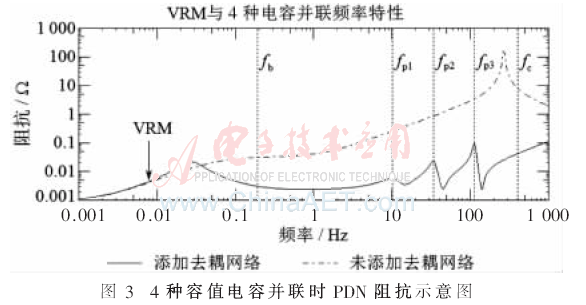
低頻段由VRM與體去耦電容C0抑制電源阻抗,高頻段由電容并聯網絡實現低阻抗。fb和fc分別為起始頻率和截止頻率。對起始頻率點,由VRM與體去耦電容器并聯,此處以Cadence仿真工具所提供的VRM模型為例,如圖4所示,其中Lout和Rout分別是VRM感應點與實際負載之間的輸出電感和電阻。

為了保證設計余量,以VRM與體去耦電容器并聯諧振阻抗作為該點阻抗值。對截止頻率點,此時處于自諧振頻率最高的電容器的感性區段,由式(3)估算該點阻抗值。對于反諧振點(圖3中fb和fc之間的阻抗尖峰點),由式(5)計算該點阻抗值。將驗證點的阻抗值與目標阻抗比較,確定個體的有效性。
得到初代所有個體的入選概率之后,根據適應值保留最優個體。采用輪盤賭的方式選擇親代個體進行交叉重組。該過程可以采用單點交叉或者多點交叉,交叉點由隨機數決定。完成交叉重組后淘汰掉最差個體,加入最優個體補全種群,保留當前最優解。然后對種群所有個體進行swap操作,即對染色體的某兩個基因進行互換得到新個體,按照Metropolis準則計算接受概率。Metropolis準則的定義由式(7)所示:

其中P為候選解的接受概率,ΔE為新解與原解目標函數值的差,T為模擬退火的溫度參數[8]。
Metropolis準則使得在初始溫度較高時能夠以較大的概率接受較差解,而且隨著溫度的降低該接受概率將會逐漸減小。因此該算法更有可能避免陷入局部極小值,從而獲得全局最優解。
初始時設定起始溫度t0,根據經驗公式t0=kδ進行估計,其中δ為目標函數的最大差值,k為一個足夠大的系數。在每次循環時模擬物理退火過程,按照tn=λtn-1更新溫度參數。當滿足終止條件時結束程序,輸出最優個體。終止條件設定為最大進化代次和終止溫度。
采用MATLAB進行程序設計,初始時指定種群規模和可用電容器種類、編碼長度等一系列運算參數。整個算法流程圖如圖5所示。
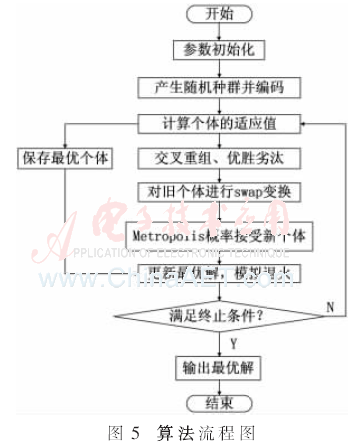
設定種群規模為50,可用電容器種類為10,限定電容器總數不超過80個,指定終止溫度和進化代數。經過30代進化后,繪制出進化代數與最優結果的進化曲線,如圖6所示。
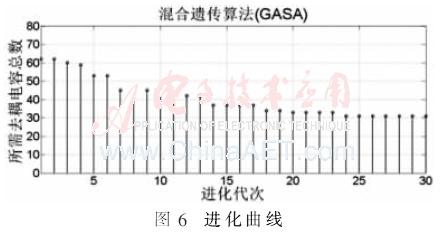
3 設計結果對比分析
為了進行對比分析,采用標準遺傳算法設計去耦網絡,同樣進行30次進化后,最終結果見表2。通常采用Cadence仿真工具進行設計時,一旦選定了足夠多可用的電容器種類,仿真工具會提供一個參考的計算結果。該方法快速直接,但通常存在設計冗余,在PCB布局空間有限的情況下完全照搬該結果可能會不現實。表2也列出了Cadence工具的直接計算結果。
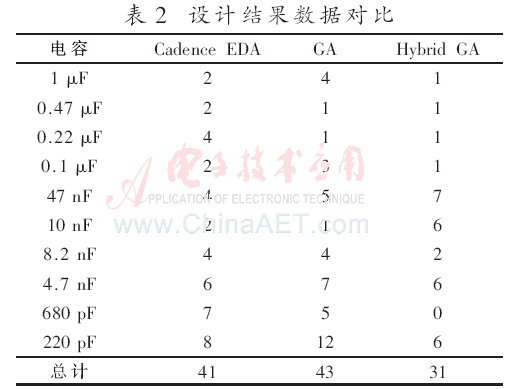
可以看到,采用混合遺傳算法最終的設計結果比仿真工具的計算結果更加合理,而標準遺傳算法在經過相同進化代次后結果存在比較明顯的冗余,這也與其全局收斂性差有關。將上述幾種去耦網絡分別進行仿真,結果如圖7所示。

由仿真結果可知,在1 kHz~500 MHz的頻率范圍內上述結果均滿足目標阻抗要求,但采用混合遺傳算法(圖中實曲線)相比另外兩種結果的設計冗余較小,減少了所需元器件數目,在PCB布局空間有限的情況下可以提供有效參考。
4 結論
本文結合基于目標阻抗的傳統設計方法,采用混合遺傳算法研究去耦電容網絡的優化設計問題。結合Cadence仿真工具對設計結果與其他方法進行了對比分析,仿真結果表明該方法所設計的去耦網絡有效、可行,避免了實際應用需要反復進行人工優化的繁瑣過程,與標準遺傳算法以及Cadence工具的計算結果相比減少了設計冗余,節省了PCB布局布線空間,為高頻電路的PDN設計提供參考。另外也可以采用其他改進算法進行更多嘗試,獲得更好的優化效果。
參考文獻
[1] 劉麗娟,楊兵初,倪蘭,等.PDN電源地平面去耦電容網絡設計[J].中南大學學報(自然科學版),2013,44(10):4088-4093.
[2] 張木水.高速電路電源分配網絡設計與電源完整性分析[D].西安:西安電子科技大學,2009.
[3] 馬秀榮,白紅蕊,白媛,等.一種抑制電源分配網絡并聯諧振的方法[J].電子技術應用,2012,38(8):59-62.
[4] WANG T K,HSIEH C Y,CHUANG H H.Design and modeling of a stopband-enhanced EBG structure using ground surface perturbation lattice for power/ground noise suppression[J].IEEE Transactions on Microwave Theory and Technigues,2009,57(8):2047-2054.
[5] CHOI J Y,MADHAVAN S.Decoupling capacitor placement in power delivery networks using MFEM[J].IEEE Transactions on Components and Manufacturing Technology,2011(10):1651-1661.
[6] 楊麗湘.基于遺傳算法的電源分配網絡設計[D].西安:西安電子科技大學,2011.
[7] 馬秀榮,孔德升,吳健.去耦電容特性阻抗反諧振點的分析與應用[J].電子技術應用,2013,39(9):61-69.
[8] 丁書斌.基于混合遺傳算法的車間調度方法研究與應用[D].大連:大連理工大學,2006.

