文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2015.07.032
中文引用格式: 敬明旻,肖莉,楊傳書. 基于最大似然估計與樸素貝葉斯的WSN故障檢測[J].電子技術應用,2015,41(7):114-117.
英文引用格式: Jing Mingmin,Xiao Li,Yang Chuanshu. Maximum likelihood estimation and Naive Bayes classifier based fault detection in WSN[J].Application of Electronic Technique,2015,41(7):114-117.
0 引言
傳感器網絡通常分布于變化劇烈、地勢復雜的環境之中。可能由于能量耗盡、外界損壞等因素導致傳感器節點出現故障,而故障節點的出現會導致路由的中斷、采集數據不完整等,因此故障節點的檢測極為重要[1]。
已有的故障檢測算法大多較為復雜[2],基于神經網絡學習[3]、Kruskal算法[4]等,此類算法均可獲得較好的檢測率,但計算冗余較高,同時需傳感節點消耗大量的能量[5]。
本文提出了一種基于樸素貝葉斯與最大似然估計的大型傳感器網絡故障節點檢查算法,算法具有如下優點:(1)所有檢測計算在sink節點中進行,從而無需消耗普通節點的能量;(2)從協議數據包中獲取端到端延遲值,從而降低節點檢測的能耗;(3)使用樸素貝葉斯分類器與最大似然估計,其計算效率較高、魯棒性好,對于大型網絡,其分類準確率好于一些復雜的分類算法。
1 樸素貝葉斯分類器與最大似然估計
1.1 故障節點引起的后果
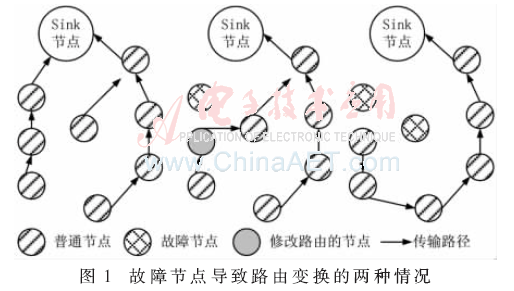
圖1所示為ZigBee規范下故障節點導致路由變換的兩種情況,ZigBee規范規定所有節點選擇最短路徑,將數據傳遞至Sink節點。從圖中可看出,故障節點導致了能耗的增加以及端到端傳遞時間的延長。
1.2 樸素貝葉斯模型

可在訓練階段使用最大似然估計(MLE)求得后驗分布,待檢測參數的值收集完畢之后,使用式(2)將其分類。
1.3 最大似然估計
一個典型WSN中一般具有大量的傳感節點,網絡中出現故障或錯誤的場景極多,因此,不可能通過大量的訓練樣本來計算所有故障場景的條件概率。本文使用MLE在利用適量的訓練樣本前提下,估算條件概率密度函數(PDF)。假設訓練屬性值集合為S={s1,s2,…,sk},將其密度表示如下:

式中S為獨立同分布。對式(4)求導可估算最大似然估計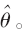
2 中心型樸素貝葉斯檢測算法
基于WSN的運行特點,假設數據包傳輸時間屬于指數級PDF,使用MLE估算訓練階段的條件概率。
圖2為算法的總體流程。
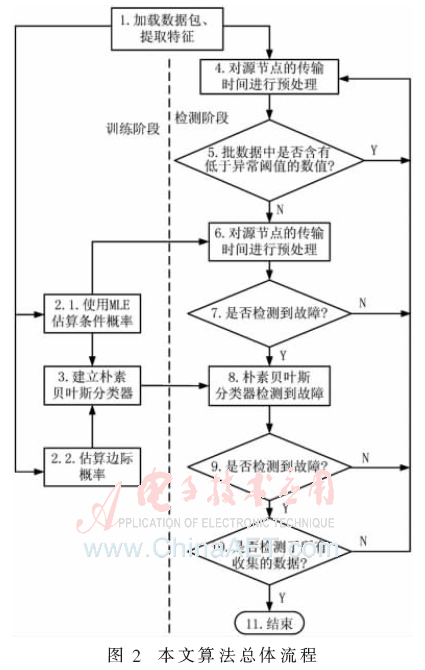
下面對程序各步驟進行詳細解釋。
步驟1:對于訓練階段與檢測階段,僅分析簡單的數據包的信息,如端到端數據包傳輸時間、源節點ID等。網絡狀態可能是正常或有錯,若類標簽是正常,網絡中則無故障傳感器;若類標簽是有錯,則網絡中含有一個以上的故障傳感器。
訓練階段:
步驟2.1:從正常類中獲取數據并開始訓練過程。當正常類數據被處理之后,提取每個節點的最小時間值作為一個異常檢測閾值。在典型的WSN拓撲結構中,各節點將若干個數據包匯聚至sink,換句話說,故障節點對傳輸的影響依賴于故障傳感器在拓撲中的位置。若故障節點是一個葉節點,則無法選擇其信號。若故障節點在通往sink節點的唯一路徑中,則該分支的節點均無法傳輸數據。
步驟2.2:根據訓練數據集的類標簽估算兩個類(正常類和有錯類)的邊際概率。
步驟3:基于步驟2.1與2.2獲得的條件概率與邊際概率建立樸素貝葉斯分類器,步驟8使用該分類器決定網絡的狀態。
檢測階段:
步驟3:sink節點將接收的數據包分批分析(1 000個數據包分為1批)。一批中根據所有數據包的端到端傳輸時間進行分組。將所有分組傳給步驟5來檢查傳輸路徑中是否含有故障節點。
步驟4:在數據包傳遞過程中,擁塞是正常情況,其端到端傳輸時間可能高于無擁塞網絡情況(其中不含有故障節點)。為了不混淆擁塞與故障節點兩種情況,將每個數據包組與其異常閾值比較。若組中所有的端到端傳輸時間均低于異常閾值,則認為路徑中至少含有一個故障傳感器,或者說,若只有一個傳輸時間值低于異常閾值,則認為是擁塞導致,而不是故障節點。
步驟5:數據包分組中可能包含不同的端到端傳輸時間值。將傳輸時間的模式值用于進一步的分析,計算每個分組中正常與故障模式值的條件概率,并與訓練PDF比較。
步驟6:如果模式值的故障條件概率高于正常模式值的條件概率,則該網絡可能有錯,否則,認為該網絡正常。
步驟7:由于錯誤設定的模式值也可能導致擁塞(并非故障節點),因此需對模式值作進一步分析。為了確定網絡狀態,將最后的5個傳輸時間使用樸素貝葉斯分類器分析。若5個時間值均較低,則使用所有的時間值來估算。由此獲得的分類器結果代替步驟7的原結果。
步驟8:如果數據包被分組定義為一個有錯網絡,對應的源節點則將被定義為可疑故障節點,然后更新該可疑故障節點。
步驟9:重復步驟5~9,直至完成所有數據包的分析。
步驟10:統計網絡狀態和可疑故障節點列表根據測試場景進行報告。
3 試驗結果與分析
3.1 仿真與試驗環境
試驗采用ZigBee系統建立WSN網絡模型,使用鄰接矩陣(傳輸成本范圍為1~200)隨機生成100個節點的網絡拓撲。網絡中僅設置一個sink節點,將sink節點的能量設為無限。各節點隨機地采集數據,然后將數據包傳遞至sink節點。試驗中設置兩個重要的網絡場景:(1)流量擁塞等級(3個流量擁塞等級):無擁塞、輕度擁塞、重度擁塞。(2)按網絡中是否有故障節點分為:故障網絡、正常網絡。試驗中將故障節點數量設為1~5個。對于100個節點的拓撲,含有1~5個故障節點,則分別有100、4 950、161 700、3 921 225、75 287 520個故障節點的位置組合,顯然,故障節點的分布情況很多,由于試驗條件限制,試驗中將故障節點組合的上限設為5 000個,因此,每個流量擁塞等級的總場景數量為20 050,3個擁塞等級則共有60 150個故障場景,每個場景傳感器共隨機產生2 000個數據包。
將本算法與其他兩個廣泛應用的性能評價算法比較:邊緣故障檢測(MFD)、歷史故障檢測(HFD)。MFD利用每個節點的正常數據,對其訓練并獲得測試數據的閾值,當擁塞導致傳輸時間變化時,選擇最小值作為閾值。若較多的新數據高于閾值,則將該傳輸路徑分類為故障路徑,將對應的源節點記為可疑節點。
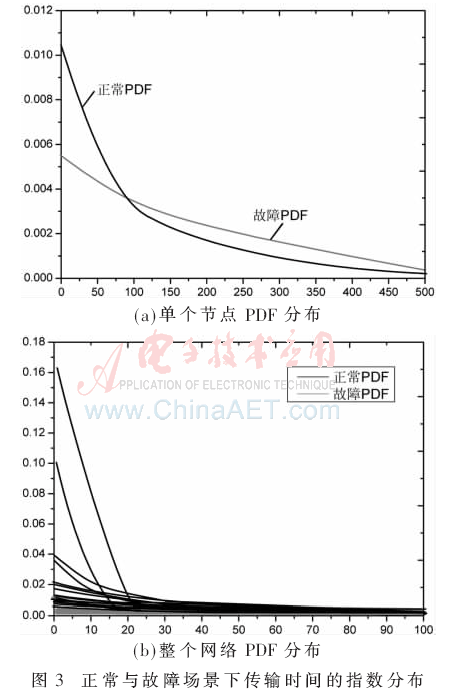
MFD使用所有正常數據訓練獲得其閾值,而HFD與本算法則使用60%左右的故障數據訓練,剩下40%故障數據用于方法驗證。在相同的流量擁塞等級下,HFD為每個源節點記錄正常與故障兩個場景的傳輸時間,若在其正常場景與故障場景中發現相同的傳輸時間,則將該網絡與源節點分別分類為故障網絡與可疑節點。圖3所示為正常傳輸時間與故障傳輸時間下指數分布MLE獲得的概率密度函數。圖3(a)中,比較了單個節點的故障場景與正常場景的PDF,圖3(b)對整個網絡的全部故障場景與正常場景的PDF進行了比較,可看出故障場景下,長傳輸時間的概率高于正常場景。
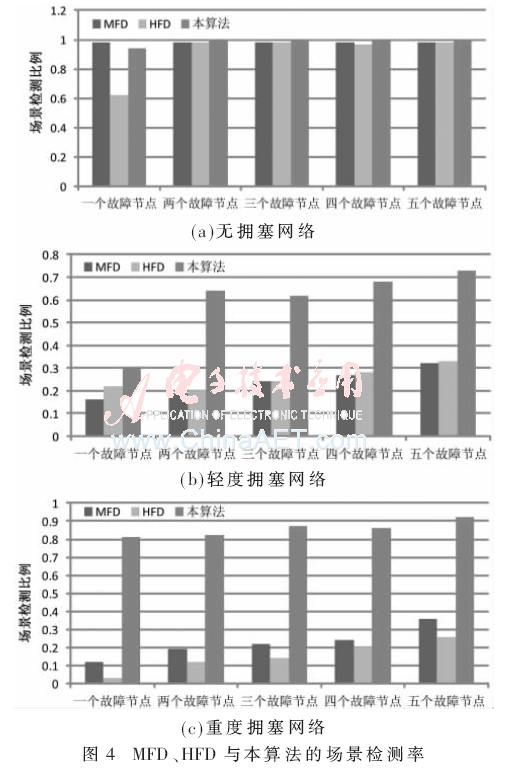
3.2 場景檢測率
本文為三個不同流量條件共產生6 015個場景。場景檢測率表示本算法檢測的可疑節點與理論故障節點匹配的數量與總場景數量的比例。圖4所示為不同流量條件下,MFD、HFD與本算法三種方法的場景檢測率。在擁塞情況下,本算法的場景檢測率最高,而其他兩種算法在輕度與重度兩種擁塞下性能不佳,因為故障的場景眾多,MFD與HFD從其數據庫中無法獲得足夠的信息來判斷傳輸時間較長的原因(因為擁塞或是因為網絡故障)。對于故障場景,輕度擁塞的一個故障節點情況下,本算法的檢測性能不佳,原因在于:一個故障節點時,故障場景有限,此時,樸素貝葉斯分類器的訓練數據不足,導致條件概率訓練不夠準確。而對于故障場景的其他情況,本算法的檢測率均高于60%,原因在于:其他情況下,利用較多的故障數據建立了條件概率,因此獲得了較高的樸素貝葉斯分類正確率。
4 結論
本文通過貝葉斯分類器與最大似然估計實現了有效的傳感器網絡故障檢測,在保持與傳統算法虛警率接近的條件下,大幅度提高了故障檢測的場景檢測率。此技術在隨鉆數據測量與風險監測方面具有廣泛應用和前景。
參考文獻
[1] 馬峻巖,周興社,李士寧,等.基于異常任務運行記錄的WSN故障檢測[J].計算機工程,2012,38(1):93-95.
[2] 李洪兵,熊慶宇,石為人,等.無線傳感器網絡中網絡層故障容錯技術研究進展[J].計算機應用研究,2013,30(7):1921-1928.
[3] 謝迎新,陳祥光,余向明,等.基于VPRS和RBF神經網絡的WSN節點故障診斷[J].北京理工大學學報,2010,30(7):807-811.
[4] 李文璟,袁野,喻鵬,等.基于改進Kruskal算法的WSN故障節點檢測方法[J].北京郵電大學學報,2014,37(4):103-107.
[5] LEE M H,CHOI Y H.Fault detection of wireless sensor networks[J].Computer Communications,2008,31(14):3469-3475.
[6] YOUN E,JEONG M K.Class dependent feature scaling method using Naive Bayes classifier for text datamining[J].Pattern Recognition Letters,2009,30(5):477-485.

