0 引言

    網線繞距指的是雙絞線扭繞之后兩個節點之間的長度，而雙絞線之間相互纏繞的緊密程度一般通過其繞距來度量^[1]。網線內部雙絞線需要相互纏繞的原因是為了減少各線之間產生的信號串擾，而每對線對采用的繞距是不同的，有著各自的標準，因此需要在網線成纜制作的同時通過實時反饋繞距值來控制成纜機制作線對。

        FPGA，即現場可編程門陣列，它是在PAL、GAL、CPLD等技術的基礎上進一步發展的可編程器件。FPGA通過為每個功能單獨地建立硬件，實現整個應用程序所需的功能，因此它具有并行處理的內在特點。硬件設計使其擁有較高的并行運行速度，同時又以其相對低廉的成本保持軟件所具有的可重新編程的靈活性。這使得FPGA非常適用于圖像處理，尤其在底層與中間層充分利用圖像處理固有的并行性特點^[2]。

1 OTSU算法

1.1 OTSU算法原理

    OTSU算法由日本學者大津展之提出，是一種自適應的閾值確定算法,又叫最大類間方差法。其基本思想是根據圖像的灰度特性,將圖像按類間距離極大準則分成目標和背景兩個部分^[3]。當目標和背景間的類間方差愈大，則表明構成圖像的兩個部分的差別就愈大,且其判斷準則簡單，易于移植至FPGA中實現，因此廣泛應用于實時圖像分割領域。

    此方法的基本原理：設待分割圖像包含L個灰度級(0，１，…，L-1)，各個灰度值的概率為：

其中n_i表示灰度值是i的像素數，N為總的像素數。給定圖像I(x，y)，目標與背景的分割閾值記作t，則屬于目標區域A與背景區域B的像素點數占整幅圖像比例分別記做：

    當使得式(8)中的類間方差達到最大，此時的t即為閾值。

1.2 簡化OTSU算法公式

    將式(7)代入式(8)可得：

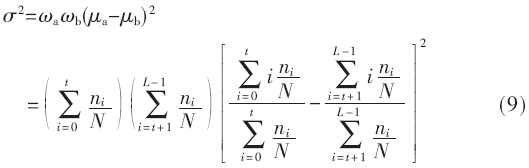
    為了簡化計算，將類間方差表達式改寫成式(10)所示。而對每幀圖像來說，N是一個常數值，可以忽略不計，從而式(10)可以進一步改寫成式(11)，便于FPGA并行實現OTSU算法。

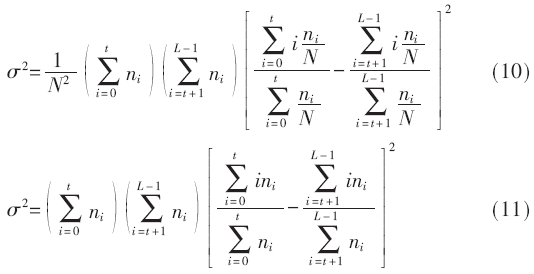
2 FPGA實時繞距檢測系統并行設計

2.1 硬件總體架構設計

    系統整體電路以FPGA為核心，其外圍的器件主要包括高速CMOS圖像采集器、串口轉無線模塊以及FPGA芯片，并在整體電路內部設計一個電源模塊為各個模塊供電。嵌入式繞距測量系統的整體框架：圖像采集部分采用高速CMOS圖像采集器，由于其有效像素點較多，一般其分別率為百萬級以上，且具有較短的曝光時間，因此被用來實時采集絞線圖像。通過使用單一的線性光源對絞線進行照射，并將其投影到事先設置好的背景板上，接著通過高速CMOS圖像采集器采集投影在背景板上的投影。最后將傳感器系統采集的圖像陣列傳輸至FPGA電路系統內，運用OTSU圖像分割算法實時二值化圖像，將二值化圖像遞交給繞距計算模塊處理，統計二值圖像的各列寬度，從而計算出相鄰最窄位置（即絞線節點）之間的距離，得到絞線的繞距值并發送至上位機。

2.2 圖像的灰度化處理

    灰度圖像是指不含彩色信息，只含亮度信息的圖像，其像素點的值稱為灰度值，范圍為0～255。由于OTSU算法是基于灰度圖像操作的，因此需要將CMOS攝像頭采集的RGB格式圖像轉換成灰度圖像。常用的灰度化處理方法有分量法、最大值法、平均值法與加權平均法。通過實驗發現，分量法無法充分利用圖像的原始信息，最大值法使得圖像亮度偏高，而平均值法則使得圖像亮度過于柔和，都不利于后續圖像分割的進行。因此，本文采用加權平均值法實現灰度化處理。

    攝像頭采集的圖像數據為3×8 bit的RGB信號，若采用常用的權值：ω_r=30%，ω_g=59%，ω_b=11%，將使得FPGA內部進行浮點乘法運算，這在消耗大量的硬件資源的同時，也拖慢了整個算法的執行速度。而采用張鵬等提出的權重^[4]，可以有效避免浮點運算，其權重分配為：ω_r=25%=2^-2，ω_g=62.5%=2^-1+2^-3，ω_b=12.5%=2^-3；則灰度值H=2^-2×R+(2^-1+2^-3)×G+2^-3×B，從而將整個運算過程轉換為1次求和運算和4次移位運算。灰度處理模塊的結構見圖1，由于采用了流水線結構的設計，即在求和運算前加入了流水線寄存器，從而在每一個周期內都能輸出一個像素點的灰度值。

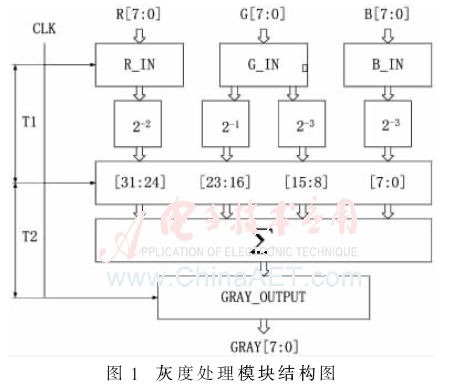
2.3 OTSU算法的硬件并行實現

    通過上述分析，可分為兩個步驟來計算類間方差：

    (1)在統計模塊中計算一幀圖像的直方圖統計、灰度統計、累積直方圖統計、累積灰度統計；

    (2)依次將累積直方圖與累積灰度統計中的數值傳入計算模塊計算類間方差。

    硬件結構框圖如圖2所示，主要由統計模塊與計算模塊構成。

2.3.1 并行統計模塊

    首先，定義一個深度為256的雙口RAM來保存每個灰度值的像素點個數，具體操作是將每個像素點的灰度值作為其中一個端口的讀地址，讀取RAM單元中的計數，將其值增加1，接著將更新后的計數從另一個端口寫入同一單元^[5]。

    其次，由于在統計處理每個像素點時，都要執行3個步驟：讀取計數、更新計數、寫回計數。只有完成當前像素點的3個步驟之后，才能進行下一個像素點的處理。而FPGA的并行特性能夠解決此類處理時延導致的低效率，即在OTSU模塊內部構建3個功能相同的統計模塊，每個模塊各自負責相鄰的3個像素點。如圖2，通過逐個激活直方圖統計1、2、3模塊，從而構成一條流水線，使得每個子模塊都有3個時鐘周期來統計1個像素點。讀取計數、更新計數、寫回計數3個步驟的邏輯被劃分到各自的時鐘周期來完成，從而提高了處理的效率。用這種方式，保證了每個時鐘周期能夠統計1個像素點。

    最后，在直方圖輸出時，使用兩個加法器將3個直方圖統計模塊的輸出結果相加，就可以計算得到完整的直方圖統計。在得到完整的直方圖之后，便可分別算出灰度統計、累積直方圖統計、累積灰度統計。

2.3.2 流水線計算模塊

    把統計模塊中的累積直方圖統計和累積灰度統計的結果依次送入計算模塊。對于計算模塊，如圖3，只需采用2個除法器和3個乘法器即可實現，并且構成一條四級流水線，這樣只需5個時鐘就能得到最終的類間方差。

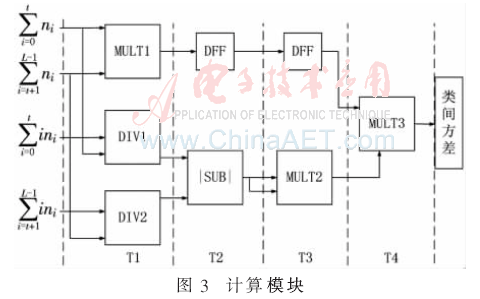
3 繞距計算模塊

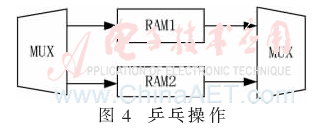
    在數字視頻處理系統中，由于數據流量非常之大且對系統的實時性的要求也較高，因此系統有必要建立高速有序的視頻數據輸入/輸出流，而乒乓緩存結構正是為平衡視頻編解碼與變速的圖像處理過程之間的速度不匹配問題提供數據通道的。

    乒乓緩存結構將輸入數據流經由數據選擇單元將數據流等時地劃分至兩個數據緩存區。采用乒乓操作^[6]處理二值化后的圖像數據如圖4所示，設置兩個BLOCK RAM：r1，r2；在第1個緩存周期，將第一幀線材每列的寬度存入r1中；待到r1存滿后，在第2個緩存周期，繼續將第二幀的線材寬度存入r2中，與此同時，對比r1中的線材寬度，找出寬度極小的n個節點，記錄n個節點的列地址，記第n個節點的列地址A1，與n-1個節點的地址A0相減即得出該線材繞距，并判斷其是否符合標準。這樣，從模塊的兩端看，輸入/輸出的數據流都是連續的，從而達到了利用低速模塊處理高速數據的目的，并加快了整個算法的實時性。

4 實驗結果與分析

    本文采用Verilog語言與C語言編寫，采用的器件是Cyclone IV EP4CE1系列的芯片。OTSU算法執行結果如圖5所示,通過換算比例尺可得出該雙絞線繞距為16.59 mm。可以看出本文算法能夠較好地分割雙絞線圖像，且具有快速的圖像處理速度，能夠實現雙絞線圖像的實時分割，使得系統能更好地檢測雙絞線繞距，達到了預期目的，而且這種方法還可以應用于其他各類線材的繞距、線寬等參數的檢測。

    通過QuartusII編譯分析可知，二值化模塊占用FPGA芯片邏輯單元不到5%，直方圖統計模塊占用了約16%，而計算模塊占用了約7%的資源，這大大節約了芯片的硬件資源，節約了硬件成本，使得更多的資源可用于其他硬件算法。對于輸入時鐘為50 MHz、大小為640×480的雙絞線圖像，每幀處理時間為：T=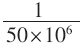×640×480=0.006 144 s，完全達到了實時進行雙絞線圖像處理的要求。

5 結論

    OTSU分割算法通過不斷計算得到使得類間方差達到最大值的閾值，其算法本身有大量操作可以并行實現。因此，相比普通的ARM平臺的順序執行方案，本文使用的FPGA方案更具實時性，能夠勝任對于網線實時繞距測量的處理速度要求。通過在FPGA中構建3個直方圖統計子模塊，使得算法在1個周期內統計1個像素點的灰度值，并使用簡化的計算公式，大大減少了算法的處理時間，并能很好地將雙絞線目標從背景中分割出來。

參考文獻

[1] 張國光.如何檢查網線性能[J].鐵道通信信號，2006，42(2)：62-63.

[2] 原魁，肖晗，何文浩.采用FPGA的機器視覺系統發展現狀與趨勢[J].計算機工程與應用，2010(36)：1-6.

[3] 齊麗娜，張博，王戰凱.最大類間方差法在圖像處理中的應用[J].無線電工程，2006(7)：25-26，44.

[4] 張鵬，鐘俊，郭安明，等.設備監控圖像預處理算法改進及其FPGA實現[J].計算機應用，2011(6)：1706-1708.

[5] BAILEY D G.基于FPGA的嵌入式圖像處理系統設計[M].原魁，何文浩，肖晗，譯.北京：電子工業出版社，2013.

[6] 吳繼華，蔡海寧，王誠.Altera FPGA/CPLD設計，高級篇[M].第2版.北京：人民郵電出版社，2011.