文獻標識碼: A
文章編號: 0258-7998(2014)07-0103-03
在近幾場局部戰爭中,數據鏈以其獨特的戰場態勢共享、精確指揮控制和武器協同的無縫鏈接優勢,將信息化作戰的特點演繹得淋漓盡致[1-2]。對裝備數據鏈系統的作戰飛機進行科學合理的效能評估,不僅對武器系統的整體性能提供了衡量標準,而且對其作戰過程中的打擊效果及作戰意圖實現提供了量化參考[3]。在作戰環境中進行效能評估,將效能評估結果運用到作戰實踐,構成了航空作戰循環體系的全過程。
在現有的文獻研究中,針對效能評估或者數據鏈體制下的效能評估問題,都只是給出一些評估方法或手段以說明不同客體的效能好壞,但是未能將評估結果加以運用;針對航空作戰的問題,一種是只注重頂層設計和戰法探討[4],而未考慮到實際效能,有的甚至缺少科學依據,另一種是研究不同作戰條件下的作戰兵力變化情況[5],而數據鏈的作用和作戰武器系統的效能考慮較少。這些基本上都只是在一個側面對航空作戰問題進行研究,對實現和把握航空作戰一體化進程的全要素分析還有一定差距,“由作戰到評估效能,再由評估結果到作戰運用”的環路尚沒有有效銜接起來。本文研究就是要實現效能評估與作戰運用的一體化。
1 飛機作戰的平均戰斗力水平
1.1數據鏈體制下的飛機效能評估
在效能評估中,飛機的空戰能力指數可以采用對數法表示為[6]:
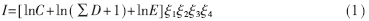
其中, I為空戰能力指數,C為機動性參數,D為火力參數,E為探測目標能力參數,ξ1為生存力系數,ξ2為電子對抗能力系數,ξ3為航程系數,ξ4為飛行員操縱效能系數。
加入數據鏈后新的空戰能力可表示為:
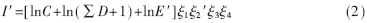
其中, E′和ξ2′分別表示經數據鏈提升后的探測能力和電子對抗能力,且E′=E+λ1E, ξ2′= ξ2+λ2ξ2,λ1和λ2表示提升率。
對于λ1的確定,考慮一種簡單的雙機協同作戰情況。假定雙機為同向直線飛行,則λ1用探測面積的變化比來表示為:
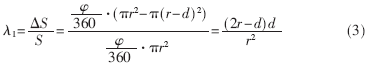
式中φ為雷達搜索方位角,r為雷達探測距離,d為機間距離(d<r)。
對于λ2的確定,在參考文獻[7]中,給出了機載電子對抗設備的電子對抗能力,全向雷達告警系統為1.05,全向雷達告警+消極干擾投放+導彈逼近警告的綜合系統為1.16~1.20,有數據鏈支撐下的電子對抗設備,還會增加積極干擾投放功能,所以對其賦值時可以使其大于無數據鏈時的電子對抗能力。
1.2 空戰能力指數到平均戰斗力水平的轉化
作如式(4)的變換,將I(I>>1)變換為在區間(0,1)上的平均戰斗力水平γ(k為一比例調節因子且k>0,作用是避免變換后的γ在數值上過于集中)。
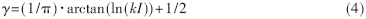
現證明γ和I關于空戰能力的描述是等價的,且γ和I具有一致性。
證明 令A={x|x∈Z, x>0}, B={x|x∈Z, 0<x<1}, 作由A到B的映射:
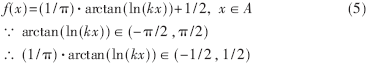
進而, (1/π)·arctan(ln(kx))+1/2∈(0,1)
所以f: A→B是由A到B的一一映射,這說明A和B是等勢(等價)的,即A~B。
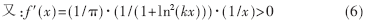
即f(x)為增函數,說明γ和I的增減變化關系一致。所以,γ在保證空戰能力指數特性的情況下,可以用來作為平均戰斗力水平。
2 空戰中的兵力變化建模
本文的建模將以藍徹斯特方程的分析方法為基礎,首先給出藍徹斯特平方律方程的表達式為:

式中R、B為紅、藍方在時刻t的戰斗單位數量,α、β為藍、紅方每個戰斗單位的平均戰斗力水平。
對上式進行等式相除后并積分,得:

令x=1-R/R0表示紅方兵力的消耗率,y=B/B0表示藍方兵力的剩余率。L=β·R02/α·B02表示紅、藍方的戰斗實力之比。將式(8)變形,用x、y、L代入得:

考慮飛機在配備有數據鏈情況下的作戰方程。首先求解平均戰斗力水平的提升率ηR和ηB,即有ηR=(γR′-γR)/γR,ηB=(γB′-γB)/γB。
在空戰中性能更優功能更強大的數據鏈擁有方可以在交戰中獲利,為此計算一數據鏈水平占優因子,將其定義為:

這樣將數據鏈體制下的雙方兵力變化規律建模為:
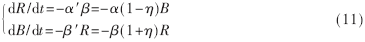
按照式(7)~(9)的分析,仍可得紅方消耗率與藍方剩余率的變化關系:
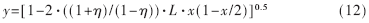
此處(1+η)/(1-η)·L部分定義為等效實力比。
在有增援的情況下建立空戰模型為:
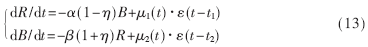
式中μ1(t)、μ2(t)表示雙方的增援率,t1、t2表示增援開始時刻,ε(t)表示階躍函數。若在戰斗中存在非戰斗減員的情況,空戰模型擴充為:
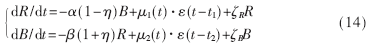
其中ζR和ζB分別表示紅、藍方的非戰斗減員系數。
3 仿真實驗
假定紅、藍方所用機型分別為米格-29和F-15E。米格-29中r=90 km,令d=70 km時,則可求λ1=0.95。設定紅、藍方電子對抗能力為1.05和1.2,紅方經數據鏈提升后變為1.8。效能評估指標中的其余參數見參考文獻[6],求解空戰能力指數(k取1/10)和平均戰斗力水平,如表1所示。

3.1戰斗實力比對雙方空戰力量的影響
取一組L=[0.6;0.8;1;1.2;1.4],由表1可知η=0.21,由此仿真得到雙方的消耗率與剩余率曲線(圖1)。
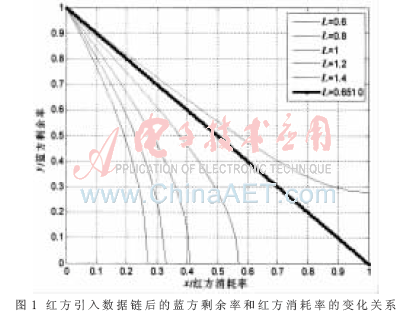
由圖知當L介于0.6與0.8之間時,達到雙方的實力平衡。令等效實力比(1+η)/(1-η))·L=1,可求得L=0.65。這說明由于數據鏈的采用,紅方只要大于藍方實力的65%就可以獲勝。圖1中也專門繪出了雙方實力的平衡的分界線。
3.2增援模型中不同增援時刻點對空戰的影響
設定增援率為2.5,且令t1=0,其他仿真參數不變,得雙方的動態損耗圖如圖2所示。
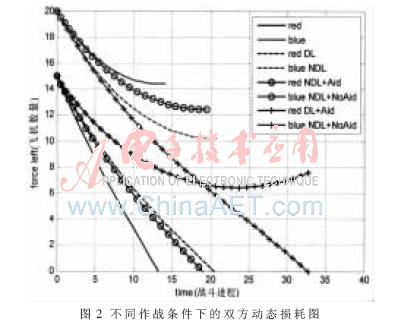
圖2中4種曲線分別為原始作戰狀態、紅方有數據鏈支持、紅方有支援但無數據鏈支持、紅方有數據鏈支持和增援。曲線說明在數據鏈體制下,紅方在增援力量幫助下可以最終獲得勝利。
接下來確定紅方有效的增援時間范圍。令t1分別為0、4、8和12,得雙方的兵力變化曲線如圖3所示。
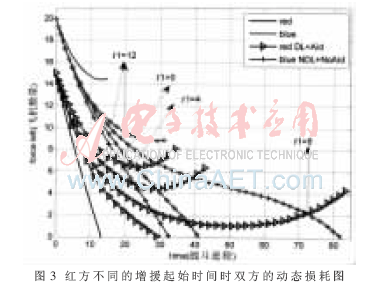
t1=12時,增援太晚已不能改變紅方失敗的結果。說明在有增援的空戰中存在一個增援的時間分界點,在此之前增援可以扭轉雙方戰局;反之不能改變戰局。在本文參數下,經多次仿真確定有效增援的時間范圍為[0,9.5]。
讓t1在[0,9.5]間取值,步進量為0.5,得到的雙方動態損耗曲線如圖4所示。
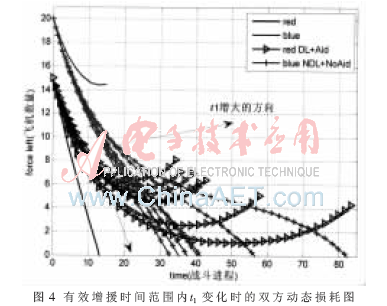
由圖知當t1增大時,總趨勢是空戰進程維持時間越長,戰斗勝利時紅方剩余的飛機數量越少。為分析不同t1時的作戰效率,這里給出隨t1值不同時紅方增援和損失飛機數量變化如圖5所示。
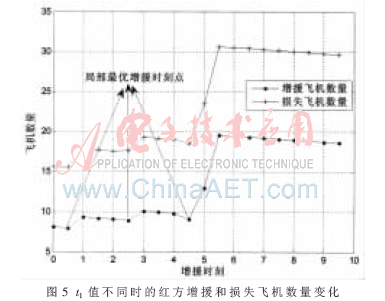
當t1變化時,增援和損失飛機數不是單調遞增關系,而是存在一系列極小值點,在這些點周圍增援和損失的飛機數都較大。據此可得,在不同的增援時刻,存在使得增援和損失飛機數同時較小的局部最優點,本文稱為“局部最優增援時刻點”。掌握了該時刻點,便于指揮員對增援時機進行把握。
對數據鏈體制下的飛機效能評估及其航空作戰運用進行了研究。給出了數據鏈體制下的飛機效能評估的計算方法,建立了反映數據鏈功能的航空作戰兵力變化模型,并考慮在有增援模式時的模型變化。仿真分析了等效實力比和數據鏈對空戰的影響,在有增援力量加入的作戰中,存在“局部最優增援時刻點”,對于空戰決策部署具有借鑒意義。
參考文獻
[1] Zhou Lei, Zhang Hanyi, Wang Tao, et al. Static check of WS-CDL documents[J]. IEEE International Symposium on Service-Oriented System Engineering, 2008(8):142-147.
[2] 曾國奇,李思吟,韋志棉,等.箭載共形相控陣衛星數據鏈通信仿真研究[J].電子技術應用,2012,38(11):104-107.
[3] 黃俊, 孫義東, 武哲,等. 戰斗機對地攻擊作戰效能分析[J]. 北京航空航天大學學報,2002,28(3):354-357.
[4] 蘇榮,滿廣志,奚丹.空天一體作戰初級階段的典型作戰運用[J].導彈與航天運載技術,2009(2):20-24.
[5] 王安麗,何勝強,張安.機群編隊對地攻擊飛機武器系統作戰模型研究[J].飛行力學,2005,23(1):82-85.
[6] 黃金才,張勇,楊磊,等.戰術數據鏈作戰效能定量評估方法[J].火力與指揮控制,2010,35(12):66-69.
[7] 朱寶鎏,朱榮昌,熊笑非.作戰飛機效能評估(第2版)[M].北京:航空工業出版社,2006.

